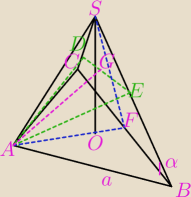
 Przez krawędź podstawy ostrosłupa prawidłowego czworokątnego poprowadzono płaszczyznę
prostopadłą do przeciwległej ściany bocznej. Oblicz pole otrzymanego przekroju, jeśli długość
krawędzi podstawy i krawędzi bocznej tego ostrosłupa wynoszą odpowiednio 10 i 13
Przez krawędź podstawy ostrosłupa prawidłowego czworokątnego poprowadzono płaszczyznę
prostopadłą do przeciwległej ściany bocznej. Oblicz pole otrzymanego przekroju, jeśli długość
krawędzi podstawy i krawędzi bocznej tego ostrosłupa wynoszą odpowiednio 10 i 13
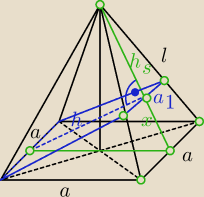 a = 10
l = 13
hs = √l2−(a2)2 = 12
a = 10
l = 13
hs = √l2−(a2)2 = 12
| x | ||||||||
= | |||||||||
| hs | a |
| 25 | ||
x = | ||
| 6 |
| hs | hs−x | ||||||||||||||
= | |||||||||||||||
|
|
| 235 | ||
a1 = | ||
| 36 |
| 5 | ||
h = √a2 − x2 = | √119 | |
| 6 |
| a+a1 | ||
P = | *h = | |
| 2 |