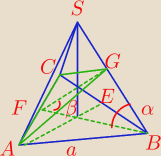
Ostrosłup prawidłowy trójkątny o krawędzi podstawy a i kącie nachylenia krawędzi bocznej do
podstawy α przecięto płaszczyzną przechodzącą przez krawędź podstawy i nachyloną do
płaszczyzny podstawy pod kątem o mierze β. Oblicz pole otrzymanego przekroju
Pomocy
nie mam pojęcia jak rozwiązać
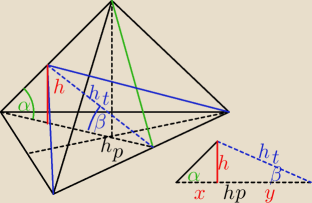
| h | |
= tgα | |
| x |
| h | |
= tgβ | |
| y |
| ⎧ | xtgα = ytgβ | |
| ⎩ | x+y = hp |
| hptgα | ||
y = | ||
| tgα+tgβ |
| hptgα*tgβ | ||
h = | ||
| tgα+tgβ |
| h | |
= sinβ | |
| ht |
| h | a√3tgα*tgβ | |||
ht = | = | |||
| sinβ | 2sinβ(tgα+tgβ) |
| a*ht | a2√3tgα*tgβ | |||
P = | = | |||
| 2 | 4sinβ(tgα+tgβ) |
