objętość bryły-współrzędne walcowe aniaaaa: obliczyc objetosc bryly V ogranoczonej powierzchniami x²+y²+4z=0 , z=1−√x²+y² korzystam tutaj ze współrzędnych walcowych czyli x=rcosα y=rsinα z=z r²=x²+y² czyli podstawiając to r² mam : z=−¹₄r² i z drugiego z=1−r i z tego można wyliczyć r czyli r∊(0,√2) z∊(−¹₄r²,1−r) i tu dla mnie zaczynają się schody jak mam wyliczyć ten kąt?

ZKS: Źle policzone r. Według mnie powinno Ci wyjść r = 2 z tego układu równań.

aniaaaa: tak masz racje źle policzyłam powinno być 2

aniaaaa: a co z tym kątem?

ZKS: Kąt się nie oblicza tylko się robi poglądowy rysunek i z rysunku odczytujesz. Według mnie φ ∊ [0 ; 2π].

aniaaaa: mozesz narysowac ten rysunek?

ZKS: x² + y² + 4z = 0 Równanie paraboloidy. z = 1 − √x² + y² Równanie stożka.

aniaaaa: ok rozumiem dziękuje

ZKS:

	2
Nie wiem czy odpowiedź dobrze wyszła V =		π?
	3

aniaaaa:

	4
mi wyszło		π
	3

aniaaaa: mam jeszcze jedno pytanie ale do zad ze wspolrzednymi biegunowymi: jezeli mam obszar y≤x²+y²≤x i y≥0 to jaki będzie ten kąt

ZKS:

	π
Według mnie φ ∊ [0 ;		] ale 100% pewności nie mam.
	2

aniaaaa:

	π
a właśnie mi sie wydaje że φ∊[0,		] ale tez pewności nie mam
	4

ZKS:

	π
A dlaczego		?
	4

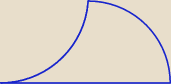
ZKS: Coś takiego dostajemy z tych nierówności.

aniaaaa: nie no strzelanie teraz to mijuż nic nie pasuje

ZKS: Chyba najlepiej będzie podzielić to na dwie części.

aniaaaa: jak chcesz podzielic na dwie części?

ZKS: D₁ :

	1
0 ≤ x ≤
	2

	1		1
0 ≤ y ≤		−		√1 − 4x2
	2		2

D₂ :

1
	≤ x ≤ 1
2

0 ≤ √x − x²

ZKS: Oczywiście D₂ :

1
	≤ x ≤ 1
2

0 ≤ y ≤ √x − x².

aniaaaa: szczerze to już w ogole nie rozumiem

ZKS: Ale czego nie rozumiesz rozbiłem ten obszar na dwie części z których łatwo policzymy teraz całki.

ZKS:

	1
Jeżeli nigdzie się nie pomyliłem to wynik		.
	4

aniaaaaa: nie rozumiem bo przechodząc na wspólrzędne biegunowe na tym obszarze mam: y≤x²+y²≤x i y≥0 czyli rsinα≤r²≤rcosα i rsinα≥0 sinα≤r≤cosα i sinα≥0 czyli r∊(sinα,cosα) i nie wiem co z tym kątem