zbadaj liczbę rozwiązań równania / dana jest funkcja wykładnicza elios: 1.zbadaj liczbę rozwiązań równania 2^x ( x² −1 ) = −1 2. dana jest funkcja wykładnicza f(x) = a^x. rozwiąż równanie f ( x+3 / x−5) =1

Basia: 1. x∊R ponieważ wypadałoby podzielić przez x²−1 musimy założyć, że x²−1 ≠ 0 ⇔ x≠ −1 i x≠1 trzeba jednak zbadać co się dzieje tych wartości x x=1 2¹*0 = −1 0 = −1 sprzeczność x = −1 2⁻¹*0 = −1 sprzeczność czyli dla x=±1 nie ma rozwiązania dla x≠±1 mamy

	−1
2x =
	x2−1

	1
2x =
	1−x2

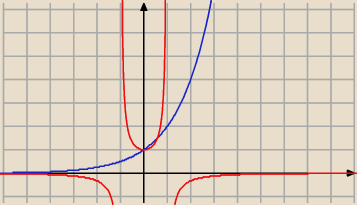
	1
rysujesz y=2x i y =
	1−x2

i odpowiedź odczytujesz z wykresu jak widać równanie ma dwa rozwiązania: x₁ = 0 x₂ nie tak łatwo wyliczyć (i nie musisz)

Basia: 2. f(x) = a^x a>0

	x+3
f(		) = a(x+3)/(x−5)
	x−5

a^{(x+3)/(x−5)} = 1 dla a=1 rozwiązaniem jest każda liczba x∊R\{5} dla a>0 i a≠1 równanie ma rozwiązanie ⇔

x+3
	= 0 ⇔ x+3=0 ⇔ x=3
x−5

elios: dzięki wielkie! Próbowaliśmy na różne sposoby, ale nie wychodziło. Teraz już wszystko jasne