Funkcja Liniowa Kinga. : Rozwiąż równanie metodą algebraiczną i graficzną: 1) 6 − l4 − xl = l2−3xl Rozwiąż równanie metodą algebraiczną i graficzną: 1)lx+2l − l2x−7l + x = 1 Jakbym mogła prosić o dokładny zapis na rozwiązania z narysowaną osią czasu.

5-latek: https://matematykaszkolna.pl/strona/1807.html moze cos to pomoze

bezendu: |x+2|−|2x−7|+x=1 1⁰ (−∞,−2) −x−2−(−2x+7)+x=1 −x−2+2x−7+x=1 2x=10 x=5∉(−∞,−2) 2⁰ <−2;3,5) x+2−(−2x+7)+x=1 x+2+2x−7+x=1 4x=6 x=1,5∊<−2;3,5) 3⁰ <3,5;∞) x+2−2x+7+x=1 9=1 sprzeczne

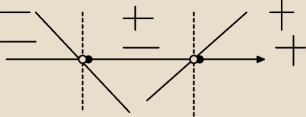
Kinga. : tak pomoże tylko chodzi o to, że ja mam to zrobić takim sposobem: lx−1l + lx+3l = 4 I. dla x∊(−∞;−3) v II. dla x∊<−3;1) v III. dla x∊<1;+∞) 1−x + (−x−3) = 4 v 1−x + x+3 = 4 v x−1 + x+3 = 4 −2x = 6 v 4 = 4 v 2x = 2 x = −3 v x∊<−3;1) v x = 1 x nie∊(−∞;−3) Odp: x∊<−3;1> tam na osi pierwszy punkt wynosi −3 a drugi 1

Kinga. : jakbym mogła prosić o wyjaśnienie w ten sposób tamtych przykładów co wcześniej podałam

bezendu: Rozpisałem Ci krok po kroku przecież ? Czego konkretnie nie rozumiesz ?

Kinga. : skąd tam się wzięło w 1. mi wyszło, że to powinno być x∊(−∞,−1)

bezendu: W pierwszym ? Pytasz o moje rozwiązanie ?

Kinga. : tak o twoje rozwiązanie

bezendu: Rozpatruje w przedziale (−∞,−2) wyrażenia są ujemne, więc opuszczając moduł zmieniam znaki.

bezendu: Popatrz post 5−latek podał Ci link, tam Pan Jakub świetnie wytłumaczył krok po kroku