Oblicz promień kuli
Artemis: Krawędź podstawy ostrosłupa prawidłowego ma długości 6, a jego ściany boczne są nachylone do
podstawy pod kątem 45 stopni. Oblicz promien kuli wpisanej w ten ostrosłup.
Proszę o rozwiązanie...
6 paź 18:40
Beti: ostrosłup prawidłowy... jaki

6 paź 18:46
Artemis: czworokątny, przepraszam, zjadło mi się słówko

6 paź 18:49
Beti:
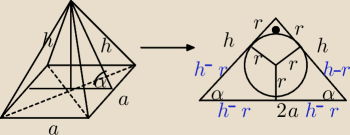
w przekroju mamy okrąg wpisany w trójkąt prostokątny równoramienny.
więc:
z tw. Pitagorasa: 2h
2 = 12
2
2h
2 = 144 /:2
h
2 = 72
h = 6
√2
z własności: 2(h − r) = 2a /:2
h − r = a
6
√2 − r = 6
r = 6
√2 − 6
6 paź 19:13
Artemis: 3(√2−1) znalazłam taką odp w ksiązce, coś mi sie tu nie zgadza...:<
6 paź 20:30
Artemis: r= 3({p}2−6)
trzeba to podzielic przez 2? Nie rozumiem...
6 paź 20:36
5-latek: Odp to 6(√2−1) bo 6√2−6 = wyciagam wspolny czynnik 6 przed nawias i mam 6(√2−1)
6 paź 20:41
nig: czyli nie ma żadnego błędu w obliczeniach? To najwidoczniej błąd w druku...
6 paź 20:45
nig: masz, zmień sobie− nie zawsze w odpowiedziach jest dobrze napisane.
6 paź 20:46
dero2005:
z tw Pitagorasa
2h2 = a2
h = 3√2
h−r = a
r = 3(√2−1)
7 paź 07:47


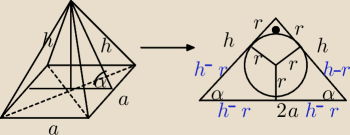 w przekroju mamy okrąg wpisany w trójkąt prostokątny równoramienny.
więc:
z tw. Pitagorasa: 2h2 = 122
2h2 = 144 /:2
h2 = 72
h = 6√2
z własności: 2(h − r) = 2a /:2
h − r = a
6√2 − r = 6
r = 6√2 − 6
w przekroju mamy okrąg wpisany w trójkąt prostokątny równoramienny.
więc:
z tw. Pitagorasa: 2h2 = 122
2h2 = 144 /:2
h2 = 72
h = 6√2
z własności: 2(h − r) = 2a /:2
h − r = a
6√2 − r = 6
r = 6√2 − 6