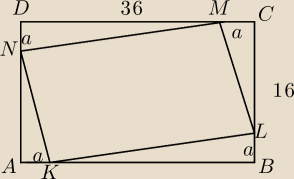
 Prostokąt ABCD ma boki długości AB=36cm i BC=16cm. Punkty K, L, M, N położone są na bokach
prostokąta ABCD w taki sposób, że AK=BL=CM=Dn= a cm. Dla jakiej wartości a pole czworokąta
KLMN jest najmniejsze?
Prostokąt ABCD ma boki długości AB=36cm i BC=16cm. Punkty K, L, M, N położone są na bokach
prostokąta ABCD w taki sposób, że AK=BL=CM=Dn= a cm. Dla jakiej wartości a pole czworokąta
KLMN jest najmniejsze?
| 1 | ||
PΔKBL= | *(36−a)*a | |
| 2 |
| 1 | ||
PΔMCL= | *(16−a)*a | |
| 2 |
| 1 | 1 | |||
PKLMN=36*16−2* | *(36−a)*a−2* | *(16−a)*a | ||
| 2 | 2 |
| 52 | ||
a= | =13 | |
| 4 |