... PuRXUTM: Witam mam taki problem x<√2−x D=(−niesk.;2] 1) dla x (−niesk.;0] x²>2−x i tak dalej... i wychodzi mi rozwiązanie x (−niesk.;−2] U (1;+niesk) uwzględniam dziedzinę i wychodzi x (−niesk;−2) 2) dla x (0;2] x²<2−x i tak dalej... i wychodzi mi rozwiązanie x (−2;1) po uwzględnieniu dziedziny x (0;1) Czyli rozwiązanie to x (−niesk;−2) U (0;1) Ale (i tu jest mój problem) jeślibym rozważał 1) x (−niesk.;0) 2) x [0;2] to bym miał inne rozwiązanie (x (−niesk;−2) U [0;1) które rozwiązanie jest prawidłowe i dlaczego ?

PW: Coś za bardzo skomplikowałeś sprawę. Wszystkie x≤0 są rozwiązaniami (bo lewa strona niedodatnia, a prawa dodatnia). Wystarczy rozwiązać nierówność na pozostałej części dziedziny, to znaczy dla x∊(0,2]. Tylko na takiej części dziedziny uprawnione jest obustronne podnoszenie do kwadratu (obie strony dodatnie).

PuRXUTM: czyli wychodzi wynik x∊(−∞;1) ? dzięki Następny mam problem ( i nie ostatni ) x²−2=−x ⇔ (to to samo co) x(x²−2)=−x² tylko dlaczego w drugim jest jedno więcej rozwiązanie

Basia: bo nie są równoważne; mnożąc obustronnie przez x musisz założyć, że x≠0 inaczej z "fałszu" zrobisz "prawdę" 3 = 5 /*0 0 = 0

PuRXUTM: dziękuje Basiu rozumiem

PuRXUTM: nastęone : narysuj wykres funkcji f(x)=log_x 7

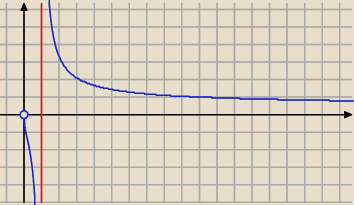Basia: x∊R₊\{1}

	1
f(x) =
	log7x

to na rysunku jest wykresem y = log_x10, ale Twój będzie podobny

PuRXUTM:

	1
dzięki nie wpadłem na to że logx 7=
	log7 x