Układ
Kostek:
Jak rozwiązać taki układ graficznie
|x|−y=1
−x+|y|=1
6 paź 17:33
Piotr 10: Można tak, że
I x ≥ 0 ⋀ y≥0 , wtedy
x−y=1
−x+y=1
II x<0⋀ y <0, wtedy
−x−y=1
−x−y=1
III x≥ 0⋀ y <0
x−y=1
−x−y=1
IV x<0 ⋀ y≥0
−x−y=1
−x+y=1
6 paź 17:37
krystek: y=IxI−1
IyI=x+1 i teraz wykresy
6 paź 17:38
Kostek:
Piotr 10 widzisz co tam widnieje ? graficznie
6 paź 17:38
Piotr 10: A co ja robię.. ?
6 paź 17:39
wredulus_pospolitus:
|x| − y = 1 −> |x| − 1 = y <−−− rysujesz
−x+|y| = 1 −> x = |y|−1 <−−−− rysujesz ... lub y = x+1 dla y≥0 i y = −x − 1 dla y<0
6 paź 17:39
Kostek:
Zrobiłeś algebraicznie, to też potrafię... Chodziło mi o sposób graficzny jak zilustrować
6 paź 17:40
Kostek:
Czemu nie można tego rysować w przedziałach ?
6 paź 17:41
Piotr 10: Właśnie chyba nie... Równie dobrze można zrobić teraz sobie tabelkę wybrać dwa punkty i
rysujesz wykresy w układzie kartezjańskim
6 paź 17:41
krystek:
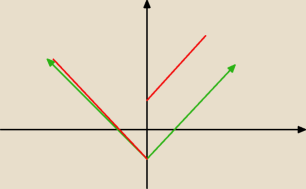
6 paź 17:41
Rafał28:
Układ przekształcasz równoważnie do:
| ⎧ | y=|x| − 1 | |
| ⎩ | |y| = x + 1 |
|
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
| ⎧ | y=|x| − 1 | |
| ⎨ | y = x + 1 |
|
| ⎩ | y ≥ 0 | |
∨
| ⎧ | y=|x| − 1 | |
| ⎨ | y = −x − 1 |
|
| ⎩ | y < 0 | |
Rozważasz te dwa przypadki graficznie w osobnych układach współrzędnych.
6 paź 17:45
krystek: W jednym ukł współrzędnych
6 paź 17:46
Rafał28:
W osobnych a suma rozwiązań to główne rozwiązanie.
6 paź 17:48
Mila:
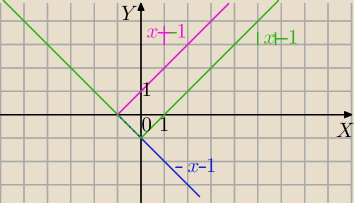
1)
y=|x|−1 Z rysowaniem nie masz kłopotu?
|2) |y|=x+1 dla tego wykresu
Rozważymy dwa przypadki:
a) y≥0 część płaszczyzny nad osią OX
y=x+1
b)y<0 część płaszczyzny pod osią OX
y=−x−1
Zbiór par (x,−x−1) i x∊<−1,0>⇔x∊<−1,0> i y=−x−1
6 paź 17:48
Kostek:
Mila teraz mam rozwiązać to algebraicznie czyli
|x|−y=1
−x+|y|=1
1. x≥0 i y≥0
x−y=1
−x+y=1
0=2 sprzeczność
2. x≥0 i y<0
x−y=1 x+1=1
−x−y=1 x=0∊<0,∞)
−2y=2
y=−1∊(−∞,0)
3.x<0 i y≥0
−x−y=1 1−y=1
−x+y=1 y=0∊<0,∞)
−2x=2
x=−1∊(−∞,0)
4.x<0 i y<0
−x−y=1/(−1)
−x−y=1
0=0 nieskończenie wiele rozwiązań
6 paź 18:06
Kostek: up
6 paź 18:30
Mila:
1) brak rozwiązań
2) x=0,y=−1
3) x=−1,y=0
4) punkt, tak.
x<0 i y<0
−x−y=1
−x−y=1 nieskończenie wiele rozwiązań, ale jakich?
y=−x−1 i −x−1<0⇔−x<1⇔x>−1i x<0⇔
x∊<−1,0> i y=−x−1
6 paź 19:23
Kostek:
4) punkt dobrze zapisałem ?
No właśnie jakich ?
6 paź 19:25
Mila:
Właśnie Ci napisałam:
y=−x−1 i −x−1<0 itd
6 paź 19:27
Kostek:
Ale czemu tak ?
6 paź 19:32
Mila: Bo rozważasz pary (x,−x−1) dla x<0 i y<0 .
6 paź 20:09
Kostek:
Nadal nie rozumiem

6 paź 20:16
Mila:
Ostatni Twój układ:
−x−y=1/(−1)
−x−y=1
Proste pokrywają się, są jednakowe, jednak taka sytuacja zachodzi dla x<0 i y<0
Każda para liczb spełniająca pierwsze równanie spełnia drugie równanie.
Masz nieskończenie wiele par , które spełniaja układ równań , jednak nie są to pary byle jakie,
ale
(x,−x−1) .
Pod warunkiem że x<0 i y<0
Po rozwiązaniu tego warunku mamy
x>−1 i x<0 i y=−x−1
6 paź 21:09
pigor: ..., taki układ rozwiązuje się algebraicznie, a znalezione jego rozwiązanie
ilustruje się na bieżąco graficznie, a więc np. tak : z własności modułu
(wartości bezwzględnej) masz kolejno równoważne koniunkcje :
|x|−y=1 i −x+|y|=1 ⇔ |x|=y+1 i |y|=x+1 ⇔
⇔ y+1 ≥1 i (x= −y−1 lub x=y+1)
i x+1 ≥0 i (y= −x−1 lub y=x+1) ⇔
⇔ y≥0 i x≥−1 i (y=−x−1 lub y=x−1) i (y=−x−1 lub y=x+1) ⇔
⇔
(x,y)= (−1,0) lub
(y≥0 i x≥−1 i y=x−1) lub
(y≥0 i x≥−1 i y=x+1) 
to tyle, teraz narysuj sobie sumę mnogościową zbioru punktów na czerwono;
i masz ilustrację geometryczną rozwiązania twojego układu równań . ...

6 paź 21:57

 1) y=|x|−1 Z rysowaniem nie masz kłopotu?
|2) |y|=x+1 dla tego wykresu
Rozważymy dwa przypadki:
a) y≥0 część płaszczyzny nad osią OX
y=x+1
b)y<0 część płaszczyzny pod osią OX
y=−x−1
Zbiór par (x,−x−1) i x∊<−1,0>⇔x∊<−1,0> i y=−x−1
1) y=|x|−1 Z rysowaniem nie masz kłopotu?
|2) |y|=x+1 dla tego wykresu
Rozważymy dwa przypadki:
a) y≥0 część płaszczyzny nad osią OX
y=x+1
b)y<0 część płaszczyzny pod osią OX
y=−x−1
Zbiór par (x,−x−1) i x∊<−1,0>⇔x∊<−1,0> i y=−x−1

 to tyle, teraz narysuj sobie sumę mnogościową zbioru punktów na czerwono;
i masz ilustrację geometryczną rozwiązania twojego układu równań . ...
to tyle, teraz narysuj sobie sumę mnogościową zbioru punktów na czerwono;
i masz ilustrację geometryczną rozwiązania twojego układu równań . ... 