Funkcja odwrotna janedoe: Hej Właśnie zaczęłam studia i już od samego początku mam kłopot z analizą matematyczną. Nie wiem, jak się zabrać za większość przykładów, bo w szkole nie mieliśmy czegoś takiego. Teraz próbuję zrobić zadania z funkcji odwrotnej i jeden przykład "zrobiłam", ale nie wiem, czy dobrze. y= log₂ (x−3) x=log₂(y−3) 2^x= y−3 y=2^x+3 Czy to jest dobrze? Z tego, co próbowałam zrozumieć funkcja musi być bijekcją, żeby dało się obliczyć funkcję odwrotną, tak? Funkcja logarytmiczna nie jest chyba, ale jak sprawdzić iniekcję i suriekcję na przykład w takim przykładzie? y= 2x² +x − 3 albo y= |x−1| Bardzo proszę o pomoc i jakieś wskazówki jak sobie radzić z takim nadmiarem materiału na studiach

wredulus_pospolitus: to jest dobrze pamiętaj jednak o dziedzinie

wredulus_pospolitus: bijekcja −−− funkcja różnowartościowa (logarytm jest ... bo to funkcja ściśle rosnąca) i 'na' także jest (jeżeli odpowiednio skonstruowana zostanie dziedzina funkcji )

wredulus_pospolitus: iniekcja (funkcja 'na') zależy od dziedziny Niektóre funkcje mogą nie być różnowartościowe (suriekcja) dla D_f=R, ale dla ograniczonej dziedziny już tak. prosty przykład: f(x) = x² <−−− nie posiada odwrotnej funkcji dl D_f=R ale dla D_f = R₊ już tak (f₋₁(x) = √x) a więc pytanie brzmi ... o jakiej dziedzinie tutaj mówimy

janedoe: No właśnie tu jest problem, bo na kartce z zadaniami nie ma podanego niczego prócz y= −4x +5, na przykład.

wredulus_pospolitus: w takim razie dziedziną przyjmujesz maksymalny przedział na którym dana funkcja jest 'na' czyli dla y=log₂x D_f = <0,+∞)

janedoe: Więc dla y=|x−1| , D_f= R⁺ ?

wredulus_pospolitus: przedział −−− rozumiemy jako słowo 'zbiór' oczywiście

wredulus_pospolitus: nie ... D_f = R ; ZW_f = R₊∪{0}

janedoe: Chyba i tak nic z tego nie zrozumiem, bo dalej nie wiem, czy ten przykład ma funkcję odwrotną czy nie...

wredulus_pospolitus: logarytm posiada funkcję odwrotną dla D_f = <0;+∞) (bądź mniejszej) ... bo dla takiej dziedziny jest 'na' (każdy 'x' ma jakiś 'y') i jest różnowartościowa (logarytm o podstawie 2 jest funkcją rosnącą)

wredulus_pospolitus: jeżeli nie masz podanej dziedziny to wybierasz maksymalną dziedzinę dla której dana funkcja jest 'na' ... i sprawdzić musisz tylko czy na tym zbiorze jest ona różnowartościowa

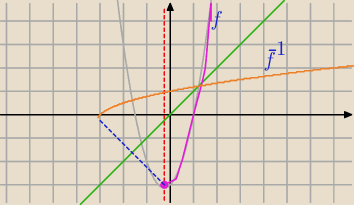
Mila: y= 2x² +x − 3 odwrotna istnieje dla funkcji różnowartościowej

	−1
xw=
	4

	−1		−1
Możesz wyznaczyć odwrotną dla x≤		lub x≥
	4		4

	−1
Rozważę przypadek dla x≥
	4

y=2x²+x−3 przedstawiam w postaci kanonicznej

	1		25
y=2(x+		)2−
	4		8

	25		1
y+		=2(x+		)2
	8		4

	1		y		25
(x+		)2=		+
	4		2		16

	1
(x+		)=√0,5y+25/16
	4

	1
x=−		)+√0,5y+25/16
	4

Zamiana zmiennych

	1
y=−		+√0,5x+25/16 wykres symetryczny do wykresu f(x)=2x2+x−3 wzgledem
	4

prostej y=x

janedoe: To mi wiele rozjaśnia, ale żeby być ekspertem to chyba jeszcze dużo zarwanych nocy przede mną heh