Zadanie Piotr 10: Naszkicuj wykres funkcji f(x)= − 2sinx*IcosxI dla x∊<−2π;2π>

	3π		π		π		3π
f(x)= − 2sin2x dla x∊<−2π;		>∪<−		;		>∪<		;2π>
	2		2		2		2

oraz

	3π		π		π		3π
f(x)=2sin2x dla x∊(−		;−		)∪(		;		)
	2		2		2		2

Narysowałem wykres funkcji, ale nie jestem jego pewny. Nie umiem tutaj narysować tego, więc prosiłbym o narysowanie tego wykresu, żebym mógł sobie sprawdzić

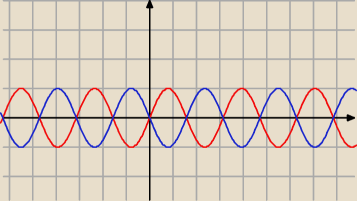
wredulus_pospolitus: ale to będzie: f(x) = +/− sin(2x) bez dwójki na początku

Piotr 10: Mi inny wykres wyszedł. Mam w przedziale <−π;0> nad osia OX te dwa ''wykresiki i w przedziale <0;II> mam na dole te dwa wykresiki

Piotr 10: Bardzo prosiłbym o narysowanie tego wykresu z wyjaśnieniem.Z góry dziękuję

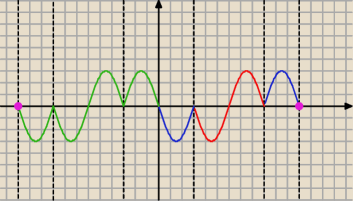
Trivial: Cześć. Ponieważ f(x+2π) = f(x) wystarczy rozważyć przedział x∊[0,2π]. W przedziale [−2π,0] wykres będzie taki sam (okresowość funkcji f). Zatem w przedziale x∊[0,2π] mamy:

	⎧	−sin(2x) dla cosx ≥ 0
f(x) = −2sinx|cosx| =	⎨
	⎩	sin(2x) dla cosx < 0

Kiedy cosx < 0 (w przedziale głównym [0,2π])? Dla x ∊ (^π₂,^3π₂). Zatem: rysujemy wykres czerwony. Dla x ∊ [0,2π]\(^π₂,^3π₂) rysujemy niebieski Teraz kopiujemy wykres na lewą stronę (nie odbijamy, tylko kopiujemy − zielony) Dodajemy fioletowe kropki, żeby było widać gdzie się kończy wykres i gotowe.

Piotr 10: Ok, dzięki . W ogóle na samym początku już błąd zrobiłem.. z tą dwójką