wykładnicza leno: Czy mając wzór funkcji f(x)= |2^x−4|+1 najpierw rysuję 2^x a potem odbijam względem osi OX i przesuwam o wektor u=[4,1]?

Basia: nie 1. rysujesz y=2^x 2. przesuwasz o wektor [0;−4] co daje y=2^x−4 3. symetria części ujemnej względem OX co daje y=|2^x−4| 4. przesunięcie o wektor [0;1] co daje y = |2^x−4|+1

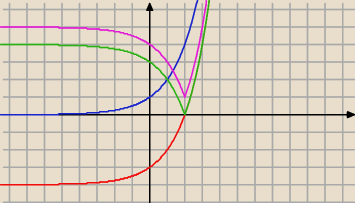
Technik: 1) 2^x niebieski 2) o 4 jednostki w dół czerwony 3) wartość bez czyli to co pod osią nad oś zielony 4) teraz wszystko o jedną jednostkę do góry różowy

leno: ah, no tak, dzięki !

leno: a jak potem określić liczbę rozwiązań f(x)=k² gdyby było f(x)=k to wiem jak zrobić, ale jeśli jest k² ?

leno: ?

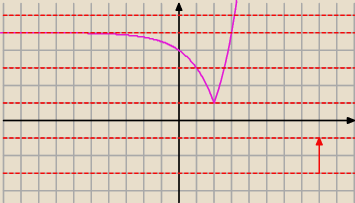
Gustlik: f(x)=k²: metoda "linijkowa: Przyłóż linijkę do wykresu i ustaw ją poziomo i przesuwaj z dołu do góry, ilość punktów przecięcia brzegu linijki z wykresem to ilośc rozwiązań dla wartości funkcji, w której brzeg linijki przecina oś OY. Wyobraź sobie, że przerywana czerwona przerywana linia −−−−−−−−−− to brzeg linijki, przesuwasz ją do góry, można więc odczytać: Spisuję po kolei: 1. dla k²<1 0 rozwiązań, 2. dla k²=1 1 rozwiązanie, 3. dla k²€(1, 5) 2 rozwiązania, 4. dla k²≥5 1 rozwiazanie. Teraz połączę przypadki z tą sama liczbą rozwiązań: 1. 0 rozwiązań dla k²<1 ⇔ k²−1<0 ⇔ (k−1)(k+1)<0 ⇔ k€(−1, 1) 2. 1 rozwiązanie dla k²=1 ⇔ k=−1 v k=1 lub k²≥5 ⇔ k²−5≥0 ⇔(k−√5)(k+√5≥0 ⇔ k€(−∞, −√5>U<√5, +∞) czyli k€(−∞, −√5>U<√5, +∞)U{−1}U{1} 3. 2 rozwiązania dla 1<k²<5 ⇔ k²>1 i k²<5 ⇔ k€(−∞, −1)U(1, +∞)∩(−√5, √5)⇔ ⇔k€(−√5, −1)U(1, √5)

leno: dzięki !