Wzory redukcyjne. vol12: Wzory redukcyjne...

	π		π
cos(8π −		) = cos( −		)
	2		2

Z racji tego, że jestem z poziomu podstawowego maty, a na polibudzie rozszerzenie przydaje się od czasu do czasu mam problem... Postanowiłem sam wypełnić niedobór mojej wiedzy z f. trygonometrycznych i...Oczywiście po kilku minutach nauki tego zagadnienia mam pierwszy problem. Skąd mam wiedzieć 7π, która to ćwiartka żeby ustalić ten ybany znak?

Basia: w tym przykładzie akurat masz 8π, które jest wielokrotnością okresu 2π czyli z definicji funkcji okresowej masz tę równość ogólnie: 1. najpierw poczytaj co to jest kąt skierowany w układzie współrzędnych (najogólniej: początkowe ramię kąta to zawsze dodatnia część OX kąty z miarą dodatnią kręcimy przeciwnie do ruchu wskazówek zegara, a te z miarą ujemną zgodnie z nim) 2. poćwicz przeliczanie stopni na radiany i radianów na stopnie (zakładam, że wiesz co to jest miara łukowa kąta) a potem poćwicz takie przykłady:

	π
−		≡ −90o czyli końcowe ramię kąta to ujemna część OY
	2

bo kręcisz kąt zgodnie z ruchem wskazówek

3π
	≡ 135o czyli końcowe ramię kąta leży w II ćwiartce
4

i tak dalej zauważ (ważne), że końcowe ramiona kątów o miarach: x i x+2kπ pokrywają się reszta musi po jakimś czasie i wykonaniu odpowiedniej liczby ćwiczeń przyjść sama

vol12: Mam jeszcze jedno pytanie... Czy tych wzorków koniecznie trzeba uczyć się na pamięć? Tego jest dużo, a ja mam do nauki masę innych rzeczy. Nie byłoby dla mnie lepiej gdzieś przeliczać sobie to na boku do postaci k90 +α?

vol12: Przeliczanie stopni na radiany umiem. Dzisiaj rano się tego nauczyłem. Tylko te wzory są trudne.

krystek: Jak znasz def funkcji tryg dowolnego kąta to szybko przeliczasz widząc w układzie współrzędnych.

vol12: Hmm sprawa wygląda mizernie. Raczej w mojej głowie nie ma układu współrzędnych więc jade na pamięć. Dzięki za pomoc.

Aga1.: Wzorów redukcyjnych jest dużo, ale jak zna się pewne własności to łatwo się ich stosuje. Np. taki wierszyk. W pierwszej ćwiartce wszystkie funkcje są dodatnie , w drugiej tylko sinus, w trzeciej tangens i cotangens, a w czwartej cosinus. Teraz taki wzór ( tylko cosinus gubi minus) cos(−α)=cosα a sin(−α)=−sinα i podobnie tg i ctg.

Aga1.: Bez zrozumienia nie nauczyłabym się na pamięć.

vol12: Aga1 tylko nie bardzo wiem jak ten wierszyk ma mi pomóc...

krystek:

	y
I teraz sinα=
	r

	x
cosα=
	r

	y
tgα=
	x

	x
ctgα=
	y

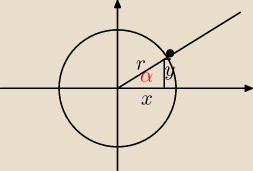
w kazdej ćwiartce patrzysz na znak x i y a r jest zawsze dodatnie.

vol12:

	π
Znaczy ja myślałem tak: najpierw policzyć ile jest		jak nieparzysta ilość to piszę
	2

kofunkcję i dalej chciałem szukać ćwiartki żeby ustalić znak. Jednak gdy mam 8π to ciężko to na oko powiedzieć. A co jeśli będzie tak z 26π.

krystek: 13*2π , czyli masz 13 obrotów i jesteś w pynkcie wyjścia

krystek: ale sin27π=sin(13*2π+π)=sinπ=0

vol12:

	10
No dobra a jak mam		π to co z tym zrobić?
	6

krystek:

	2		1
=1		π=π−		π
	3		3

krystek:

	1		1
I teraz np sin(π−		π)=sin		π ( w II ćw sin dodatni)
	3		3

	1		1
ale cos(π−		π)=−cos		π (II ćw cos ujemny)
	3		3

vol12:

	2		1
Niby skąd 1		π = π −		π
	3		3

Aga1.:

	π
I ćwiartka1 (0,		),
	2

	π
II (		,π)
	2

	3
III (π,		π)
	2

	3
IV ćwiartka (		π,2π)
	2

	2		1
1		π=2π−		π
	3		3

Końcowe ramię leży w IV ćwiartce, a w czwartej tylko cosinus jest dodatni. Najpierw ustalasz znak, a później sprawdzasz, czy funkcja przechodzi w kofunkcję ,czy nie.

krystek: Ale bzdurę wczoraj napis lam . Poprawiam

	2		1
1		π=2π−		π (dzięki Aga1 ,że porawiłas)
	3		3

I teraz

	2		1		1
sin1		π=sin(2π−		π)= sin		π
	3		3		3

krystek:

	1
i zgubiłam "−" =−sin		π
	3