liczby zadanie: 1.Czy w n−kącie foremnym istnieje przekątna o długości równej promieniowi okręgu opisanego na tym n−kącie, jeżeli a) n = 2016 ; b) n = 2014 ; c) n = 2013 ; d) n = 2010 ? na zajeciach bylo, ze liczba wierzcholkow musi byc podzielna przez 6 ale dlaczego? 2. W dowolnym zbiorze złozonym z 19 liczb całkowitych dodatnich istnieja dwie liczby, których róznica jest podzielna przez m i jest podzielna przez n. Czy powyzsze zdanie jest prawdziwe dla a) m=6, n=8 ; b) m=4, n=6 ; c) m=6, n=9 ; d) m=4, n=5 ? byla mowa o NWW i o tych samych resztach z dzielenia ale ja nie zrozumialem 3.Czy dla dowolnych liczb rzeczywistych dodatnich x, y, z prawdziwa jest nierównosc a) xyz <x³+y³+z³ ; b) xyz <x²+y²+z² ; c) xyz <x⁵+y⁵+z⁵ ; d) xyz <x⁴+y⁴+z⁴ ? 4.Czy dla dowolnych liczb rzeczywistych dodatnich x, y, z prawdziwa jest nierównosc a) 2013xyz >x³+y³+z³ b) 10xyz >x³+y³+z³ c) xyz >x³+y³+z³ d) 3xyz >x³+y³+z³ ?

zadanie: prosilbym o pomoc w tych zadaniach

zadanie: ?

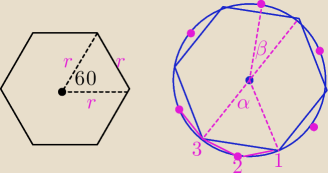
Mila: 1) Aby cięciwa (przekątna ) była równa promieniowi, to musi łączyć końce promieni z kątem środkowym60⁰. Tak jest w dwunastokącie foremnym, łączymy co drugi wierzchołek. Sześciokąt foremny jest wpisany w dwunastokąt foremny. a)n=2016 2016=6*336 tak Ci podano na wykładzie. Ja liczę tak:

	360
β=
	2016

360
	*k=60 /:60 i k∊C Czy z kątów środkowych (=β) można utworzyć kąt środkowy 60?
2016

6
	*k=1⇔6*k=2016
2016

	2016
k=		=336
	6

odp. Tak Wiesz dlaczego dzielimy przez 6?

zadanie:

	1
bo ten kat musi byc oparty na		okregu?
	6

zadanie: jezeli to mozliwe to poprosilbym o wytlumaczenie 2 zadania

zadanie: ?

zadanie: dobrze jest to co napisalem o 10:24?

Mila: 10:24 dobrze , masz otrzymać kąt środkowy 60⁰ przy połączeniu cięciwą odpowiednich wierzchołków. a) jeśli liczbę całkowitą dzielimy przez 6, to mogą być reszty: 0,1,2,3,4,5 Wśród 7 liczb całkowitych istnieją zatem dwie liczby takie ,że ich różnica jest podzielna przez 6 Przynajmniej jedna z reszt musi się powtórzyć. Jeśli liczbę całkowitą dzielimy przez 8, to mogą być reszty: 0,1,2,3,4,5,6,7 Wśród 9 liczb całkowitych istnieją zatem dwie liczby takie ,że ich różnica jest podzielna przez 8. Przynajmniej jedna z reszt musi się powtórzyć. W tym zadaniu masz znaleźć takie a i b , aby a−b dzieliło się przez 6 i przez 8 ( czyli było wielokrotnością 6 i 8) a−b=6k /*4 i k∊C a−b=8p /*3 i p∊C 4a−4b=24k 3a−3b=24p a−b=24(k−p) a) wsród 25 dowolnych liczb całkowitych można znaleźć a i b, takich aby a−b było wielokrotnością 24 odp. wśród 19 liczb − nie. b) NWW(4,6) =12 Wśród 13 liczb całkowitych istnieją zatem dwie liczby takie ,że ich różnica jest podzielna przez 6 Przynajmniej jedna z reszt musi się powtórzyć. Tym bardziej wśród 19 liczb. odp. tak dokończ

Mila: A tu spojrzałeś?

zadanie: tak widzialem dziekuje ale zastanowie sie nad tym w piatek bo teraz mam inne zadania

Mila: Jakie masz podane prawidłowe odpowiedzi. Napisz w piątek.

zadanie: c) NWW(6,9)=18 odp. tak d) NWW(4,5)=20 odp. nie