Naszkicuj wykres funkcji Mistrzu: Witam ma zadania z analizy matematycznej i ich kompletnie nie rozumię: Naszkicuj wykres funkcji: f(x)=¹_|x|−1 f(x)=tg(x)−1 f(x)=(x−1)³ f(x)=x³−1 f(x)=|e^x −1| f(x)=^|x|_x f(x)=^x−2_x−1 f(x)=ln(x−2) f(x)={|x|}−1 f(x)=¹_x² f(x)=¹_sin(x) f(x)=^2x−1_x−3 f(x)=|^x+3_x−1| f(x)=¹_cos(x) f(x)=¹_x² f(x)=−ctg|x| f(x)=||x|−1|−2 f(x)=−√|x| f(x)=|sng(x+3)| f(x)=|¹_x+2| f(x)=|(x+3)³| f(x)=(|x|−1)² f(x)=sgn(|x|+2) Nom, trzeba narysować funkcję ale tez trzeba narysować np. f(x)=¹_|x|−1 y₁=¹_x−1 y₂=¹_|x|−1

Patryk: na zadania z analizy to to nie wygląda

Trivial: Nie rozumiem czego nie rozumiesz.

Mistrzu: nie byłem na 2 lekcja, gdyż byłem w sądzie na rozprawie jako świadek a ja jestem 1 LO i mamy wstęp do analizy matematycznej

Aga1.: Nie mogę uwierzyć,że takie zadania są w pierwszej klasie liceum.

Basia: wszystko co dotyczy funkcji ∊ analizy matematycznej także to

Basia: oczywiście, że nie Ago niby skąd w 1 LO mają wiedzieć co to jest sinus, cosinus, tangens, liczba Eulera, signum i tak dalej wstydzimy się przyznać, że studiujemy, a czegoś tak prostego nie umiemy ?

Mistrzu: Proszę uwierzyć że to jest w 1 LO, gdyż to LO jest inne od normalnych

Aga1.: A cóż to za liceum ? Napisz coś więcej o nim , może to klasa uniwersytecka?

wzory: Wybiórcze przykłady są trudne te które napisała Basia reszta do zrobienia na poziomie lo

Mistrzu: tak to klasa UNIWERSTYTECKA we Wrocławiu

Mistrzu: tak to klasa UNIWERSTYTECKA we Wrocławiu

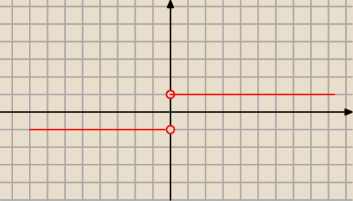
Aga1.: Rozwiążę

	IxI
np. f(x)=		, x≠0
	x

	x
f(x)=		=1, gdy x>0
	x

	−x
f(x)=		=−1, gdy x<0
	x

Basia: XIV (o ile dobrze pamiętam) LO we Wrocławiu. Chodzą tam ludzie wybitnie uzdolnieni matematycznie, zajęcia prowadzą naukowcy z UWr.

Mistrzu : tak, tak na jednym z wykładów nie byłem no i. ..

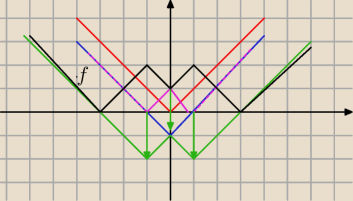
Aga1.: f(x)=IIxI−1I−2I y₁=IxI y₂=IxI−1 kolor niebieski y₃=IIxI−1I różowy y₄=IIxI−1I−2 I ostatecznie f(x)=−−−−− kolor czarny

Mistrzu : no niektóre zrobiłem a niektórych nie jestem pewien a najbardziej tych ulamkowych np. ¹_x²

Basia: te, w których nie masz ani |...|, ani wyraźnego przesuwania

	1
np; f(x) =		najlepiej będzie zrobić układając tabelkę częściową
	x2

musisz się sam przekonać jak te wykresy powstają

	1		1
to samo dotyczy f(x) =		i f(x) =
	sinx		cosx

	1
dla f(x) =		zrób sobie wykres w przedziale (0;π)∪(π;2π); potem wszystko się powtarza
	sinx

bo to funkcja okresowa tak samo jak zwykły sinus

	1
dla f(x) =		w przedziale (−π2;π2)∪(π2;3π2)
	cosx

(łatwiej niż w (0;π)∪(π;2π)); potem jak wyżej

Mistrzu : a właśnie z modułem i Przesuwaniem w liczebniku i mianowniku to jak? bo nie wiem jak to rozpisać na te mniejsze równania

Basia: może podaj konkretny przykład (jeden) za dużo tam tego i już się pogubiłam

Mistrzu : f(x)= ^2x−1 _x−3

Basia:

	a
zakładam, że wiesz jak narysować wykres funkcji g(x) =
	x

(bo już powinieneś)

2x−1		2(x−3)+5		2(x−3)		5		5
	=		=		+		=		+ 2
x−3		x−3		x−3		x−3		x−3

	5
1. rysujesz wykres g(x) =
	x

	5
2. przesuwasz o wektor u→=[3; 2] i dostajesz f(x) = g(x−3)+2 =		+2
	x−3

i tyle

Aga1.:

	x−2
f(x)=
	x−1

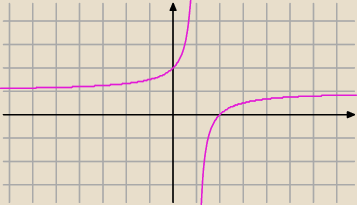
x−2		x−1−1		x−1		1		1
	=		=		−		=		+1
x−1		x−1		x−1		x−1		x−1

Aga1.:

	1
f(x)=I		I
	x+2

Aga1.:

	1
y1=		−−−kolor szary
	x

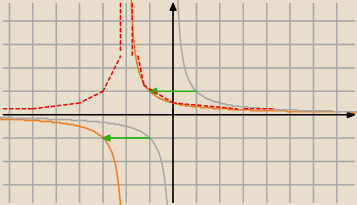
	1
y2=		kolor pomarańczowy
	x+2

f(x) czerwony