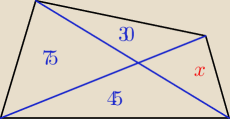
 Przekątne czworokąta dzielą ten czworokąt na cztery trojkąty. Dane sąpola trzech trójkątów.
Oblicz pole czwartego trójkąta.
Przekątne czworokąta dzielą ten czworokąt na cztery trojkąty. Dane sąpola trzech trójkątów.
Oblicz pole czwartego trójkąta.
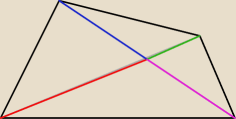 a − długość czerwonego odcinka
b − długość niebieskiego odcinka
c − długość zielonego odcinka
d − długość różowego odcinka
α − miara kąta ostrego między przekątnymi czworokąta
180o − α − miara kąta rozwartego między przekątnymi czworokąta
Z wzorów na pole trójkąta mamy :
1) 0,5 ab sin α = 75 ⇒ ab sin α = 150
2) 0,5 bc sin( 180o − α) = 30 ⇒ bc sin α = 60; bo sin ( 180o − α) = sin α
3) 0,5 ad sin ( 180o − α) = 45 ⇒ ad sin α = 90
Dzielimy stronami:
a − długość czerwonego odcinka
b − długość niebieskiego odcinka
c − długość zielonego odcinka
d − długość różowego odcinka
α − miara kąta ostrego między przekątnymi czworokąta
180o − α − miara kąta rozwartego między przekątnymi czworokąta
Z wzorów na pole trójkąta mamy :
1) 0,5 ab sin α = 75 ⇒ ab sin α = 150
2) 0,5 bc sin( 180o − α) = 30 ⇒ bc sin α = 60; bo sin ( 180o − α) = sin α
3) 0,5 ad sin ( 180o − α) = 45 ⇒ ad sin α = 90
Dzielimy stronami:
| a | 150 | 5 | 2 | |||||
1) przez 2) | = | = | ⇒ c = | a | ||||
| c | 60 | 2 | 5 |
| b | 150 | 5 | 3 | |||||
1) przez 3) | = | = | ⇒ d = | b | ||||
| d | 90 | 3 | 5 |
| 2 | 3 | 6 | ||||
Px = 0,5 cd sin α = 0,5 * | a * | b sinα = | *0,5 ab sin α = | |||
| 5 | 5 | 25 |
| 6 | ||
= | *75 = 6*3 = 18 | |
| 25 |
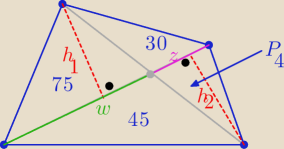 Inny sposób:
Inny sposób:
| 1 | 1 | h1 | 30 | ||||
*w*h1=75 i | *z*h1= 30 ⇒ | = | |||||
| 2 | 2 | h2 | 75 |
| 1 | 1 | h1 | P4 | |||||
i | *w*h2= 45 i | *z*h2= P4 ⇒ | = | |||||
| 2 | 2 | h2 | 45 |
| 30 | P4 | 30*45 | ||||
zatem: | = | ⇒ P4= | = .... = 18 [j2] | |||
| 75 | 45 | 75 |

| 75 | 45 | ||
= | ⇔x=18 | ||
| 30 | x |

| w | 30 | |||
Poprawię zapisy: ⇒ | = | |||
| z | 75 |
| w | P4 | |||
⇒ | = | |||
| z | 45 |
| 30 | P4 | |||
to | = | ⇒ P4= 18 | ||
| 45 | 30 |
