m=? bla bla: Dla jakich wartości parametru m, m∊R, równanie m*16^x + (2m−1)*4^x+2−3m=0 nie ma pierwiastków rzeczywistych?

Eta: Podpowiadam

Eta: Witam Domyslam sie ,że jesteś maturzystą , więc podam tylko wskazówki. Myślę ,że poradzisz sobie w dalszych obliczeniach? po pierwsze : zobaczmy co bedzie sie działo dla m = 0 otrzymasz: − 4^x +2 =0 => 4^x = 2 => x = ¹₂ więc jest pierwiastkiem rzeczywistym zatem , już wiemy ,że : m ≠0 równanie jest typowym : 16^x = t² i 4^x = t zatem nie będzie rozwiazań , gdy t₁ ≤0 i t₂≤0 ponieważ otrzymamy równanie kwadratowe z niewiadomą "t" i parametrem "m" m*t² +( 2m −1)*t +2 −3m =0 to; nie będzie rozwiązań gdy : spełniony będzie układ warunków: 1/ m≠0 −−−− to już sprawdzaliśmy i 2/ Δ <0 wyznacz Δ powinna wyjść : 16m² − 12m +1 zatem: Δ<0 <=> 16m² − 12m +1 <0 odp.2/ podaj przedział dla "m" następnie: gdy Δ ≥0 −−− będą dwa t₁ i t₂ , i mają być obydwa ujemne spełniające warunki: 1/ Δ≥0 i 2/ t₁ +t₂ ≤0 i 3/ t₁*t₂ ≥ 0 −−− tu zastosuj wzory Viete^'a i podaj cz. wspólną jako ostateczną odp: podaj cz. wspólną wszystkich warunków, wymienionych od samego początku. PS; liczyłam , obliczenia troszkę nieciekawe ( chciałoby się "ładne") ale myslę ,że poprawna odp ( jak się nie pomyliłam?) to:

	3 −√5		2
m€ <		,		>
	8		3

Może jeszcze Bogdan zweryfikuje i sprawdzi

Eta: teraz wychodzę na chwilę ..... na dobrą herbatkę .

bla bla: tak jestem maturzystką wsdzystko zrozumiałam mniej wiecej wiedziałam jak sie takie zadania rozwiązuje ale właśnie wychodziły mi nieciekawe wyniki i jak się okazało, zła odpowiedż. Ale tutaj Tobie odpowiedz wyszła dobra tylko, że ze strony lewej przedział ma być otwarty.... dziekuje baaardzo serdecznie za pomoc i smacznej herbatki życzę

bla bla:

	1		3+√5
coś mi nie wyszło w ostatecznej odp.:( moje rozwiązanie to m∊(		;		)
	2		8

	3−√5		3+√5
w założeniu Δ<0 m∊(		;
	8		8

	1		2
a gdy Δ≥0 m∊(		;		)
	2		3

w którymś coś pokreciłam

Eta: podpowiem:

	3 −√5
		≈ 0,1
	8

3 +√5
	≈ 0, 65
8

teraz już banał ... czy tak?

	3 −√5		2
cz. wspólna zatem jest: m€<		,		>
	8		3

	1		2
powinnaś napisać dla Δ≥0 ,żze m€ <		,		[C[>
	2		3

i wszystko gra

Eta: znowu chochlik

	1		2
m€<		,		>
	2		3

Eta:

	3 −√5		2
Odp: dla m€<		,		> równanie nie ma pierwiastków rzeczywistych
	8		3

czy teraz już jasne?

bla bla:

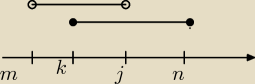
	3−√5
m=
	8

	1
k=
	2

	3+√5
j=
	8

	2
n=
	3

bla bla: dobrze zaznaczyłam? bo już zgłupiałam...:(

Eta: Poczekaj chwilę , sprawdzę , bo coś mi tu namieszałaś zasugerowałam się Twoją odpowiedzią ., ale coś mi tu nie pasuje.

AROB:

	1		3+√5
A mnie wyszło: m∊ <		,		)
	2		8

bla bla: no właśnie mi tak samo jak AROBowi tlyko, że to nie jest poprawna odpowiedz... Eta podała na początku poprawną...

Eta: Tak masz rację

	3 +√5
poprawna odp: m€< 12,		>
	8

popraw , bo przedział domknięty pora spać , zmęczenie robi swoje Dobranoc!

Eta: Macie rację

Eta: Myślę ,że zaraz będzie "wejście smoka" i wszystko sie wyjaśni

bla bla: Dobranoc Eta

	3−√5		2
tylko, że w odpowiedziach jest m∊(		,		>
	8		3

dobra już Was nie mecze z tym może jest bląd w odpowiedziach...