 Dany jest trojkat prostokatny ABC. symetralna przeciwprotokatnej AB dzieli jedna z
przyprotokatnych na odcinki dlugosci 3 i 6cm. wyznacz długosc drugiej przyprotokatnej i
przylegly do niej kat ostry.
Dany jest trojkat prostokatny ABC. symetralna przeciwprotokatnej AB dzieli jedna z
przyprotokatnych na odcinki dlugosci 3 i 6cm. wyznacz długosc drugiej przyprotokatnej i
przylegly do niej kat ostry.
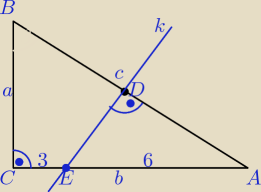 k − symetralna boku c, czyli punkt D − to środek boku c.
ΔABC ∼ ΔADE
k − symetralna boku c, czyli punkt D − to środek boku c.
ΔABC ∼ ΔADE
| b | |||||||||
Stąd: | = | |||||||||
| 6 | c |
| c | ||
c * | = 6 * 9 ⇒ c2 = 108 ⇒ c = 6√3 cm | |
| 2 |
| a | 3√3 | 1 | ||||
cosβ = | = | = | ⇒ β = 600 | |||
| c | 6√3 | 2 |

