Nie śpię bo liczę Δ Nie śpię bo liczę Δ: Dla jakich wartości parametru a równanie |x−1|=a²−4a−1 ma dwa dodatnie pierwiastki ogólnie żeby to miało dwa rozwiązania to a²−4a−1>0 wtedy mam dwa rozwiązania ale jaki warunek na dwa dodatnie ?

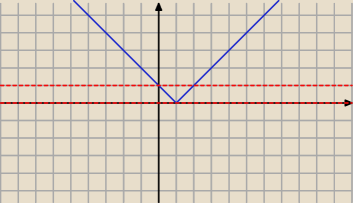
Godzio: Takie coś rozwiązuje się najlepiej na rysunku 0 < a² − 4a − 1 < 1

Nie śpię bo liczę Δ: Ale ja muszę zrobić to algebraicznie ? I czemu masz prostą skoro a²−4a−1 to będzie parabola ?

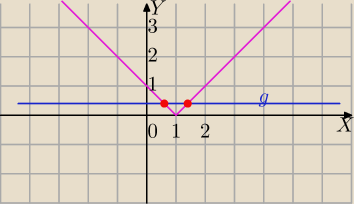
Mila: f(x)=|x−1| g(m)=a²−4a−1 g(m)>0 i g(m)<1

Godzio: Ale ta parabola ma się znajdować między 0, a 1 żeby były 2 dodatnie rozwiązania. Przyjmijmy: a² − 4a − 1 = k. Wedy: |x − 1| = k 2 dodatnie rozwiązania ma gdy k ∊ (0,1). Teraz lepiej ?

ZKS: Najlepiej graficznie ale jak już trzeba koniecznie algebraicznie to |x − 1| = a² − 4a − 1 dwa rozwiązania mamy kiedy a² − 4a − 1 > 0 rozbijając wartość bezwzględną dostajemy x − 1 = a² − 4a − 1 ∨ x − 1 = −a² + 4a + 1 x = a² − 4a ∨ x = −a² + 4a + 2 aby pierwiastki były dodatnie to a² − 4a > 0 ∧ −a² + 4a + 2 > 0. Wszystko zbierasz w całość i masz odpowiedź. Tylko zobacz ile dłużej robisz algebraicznie niż graficznie.

Nie śpię bo liczę Δ: Tylko graficznie nie podam parametru i tu jest haczyk

ZKS: Jak nie podasz parametru? Przecież Godzio i Mila napisali jak zrobić graficznie.

Nie śpię bo liczę Δ: Wszystko czyli część wspólną a²−4a>0 i −a²+4a+2>0 vzyli ten pierwszy warunek a²−4a−1>0 nie jest w sumie potrzebny ?

ZKS: Jest aby istniały dwa pierwiastki.

Nie śpię bo liczę Δ: A przedziału nie podam bo odpowiedź to (2−√6;2−√5)∪(2+√5;2+√6) i dlatego sposób graficzny jest do bani

Godzio: Przecież to funkcja kwadratowa, to w czym problem rozwiązać takie nierówności, które podałem na początku ?

Nie śpię bo liczę Δ: Jeszcze jedno pytanie Czemu nie mogę rozpatrywać tylko warunków a²−4a>0 i −a²+4a+2>0

ZKS: Jeżeli rozwiązujesz algebraicznie to od razu na samym początku należy założyć że a² − 4a − 1 jest większe od 0 ponieważ tylko wtedy mamy dwa rozwiązania. Jeżeli graficznie to pokazujesz na rysunku tak jak Godzio i Mila to zrobili.

Nie śpię bo liczę Δ: ZKS i potem muszę też rozważać do części wspólnej a²−4a−1>0 Daj już spokój tym graficznym nie chcę robić graficznie...

ZKS: Graficznie najszybciej i chyba najlepiej ale jak kto woli. Tak też musisz bo muszą być spełnione wszystkie warunki.