hej ponownie ;) Antoninette: mam jeszcze dwa działania przy których się trochę gubię, a) 27^log₃2 + log₄1 =

	log75
b)		=
	log7125

dzięki wielkie za pomoc

matyk: a) skorzystaj z wzoru: a^log_ab=b

Antoninette: przy pierwszym czy w obydwóch?

bezendu: a) 8

	1
b)
	3

Eta:

	log75
b)		=....
	3*log75

Antoninette: okey czekaj ale w pierwszym wiem że log₄1 = 0 , a w tym pierwszym członie 27 mam przedstawić jako potęgę 3 czyli zapisać 3^3log₃2

bezendu: Znasz wzory ?

Antoninette: tak, ale wole mieć pewność , że dobrze robię i korzystam z poprawnego wzoru, należę do bardzo chaotycznych osób

matyk: pierwsze myślisz ok

Antoninette: to zaraz napisze co mi z tego wynikło

bezendu: Skoro znasz to nie powinno być problemu matyk praktycznie wszystko podał na tacy

matyk: wzorek do b)

	logcb
logab=
	logca

Antoninette: w pierwszym wyszło mi 6 a nie 8 zrobiłam tak : 3^3log₃2 + log₄1 = 2 * 3 + 0 = 6....

Antoninette: zajmę sie drugim w między czasie.

Eta: 3^3*log+32= 3^log₃23=2³=.....

Mila: 3log₃2=log₃(2³)=log₃(8) 3^log₃(8)=8

Antoninette: okey rozkminiam pierwsze , czyli potęgę 3 przenoszę do potęgi 2 w tym przykładzie, jako p we wzorach tak?

Antoninette: w drugim przykładzie odpowiednio rozpisałam :

	log75		log75
=		= log7
	log753		log753

Piotr 10:

log75		1		1		1
	=		*		log57=
log7125		log57		3		3

Mila: Zobacz co Eta napisała o godz.22:28.

Piotr 10: Miałem dzisiaj identyczny przykład logartymu do zrobienia na sprawdzianie

Mila: I jak Ci Piotrze poszło, czy była jakaś trudna nierówność, równanie z parametrem.?

ryjek:

	1
Siema Piotr 10 ale tak z ciekawosci skad po = wychodzi
	log57

skąd ta piątka u podstawy log

ryjek:

	1
i razy
	3

Piotr 10: Ogółem było 6 zadań, wszystkie zrobiłem. Równania z parametrem było, ale nie takie jak ostatnio mi pomagałaś robić . Była w przedostatnim zadaniu nawet trudna nierówność, bo nie mogłem znaleźć pierwiastka przez który podzieli się wielomian, ale na szczęście się udało. Z parametrem to miałem coś w stylu, że miałem dwa wykresy funkcji i miałem wyznaczyć wartość parametru m dla których wykresy funkcji przecinają się we wspólnym punkcie osi OX( coś takiego). Na początku nie za bardzo wiedziałem. Ale po chwili popatrzyłem na jeden wykres funkcji, który miałem narysowany( bo mnie proszono w podpunkcie wcześniejszym o narysowanie go) i patrze, że ten wykres przecina raz z osią OX i podstawiłem za x=0,5 i przyrównałem te dwie funkcje i wyszło

Piotr 10:

	1
Zastosowałem wzór na zmianę podstawy logartmu logab=
	logba

Antoninette: jesteście wspaniali! <3

Mila: To ostatnie zadanie z logarytmów ma dwie gwiazdki i zawsze uczniowie mają kłopoty, sama przez nieuwagę w pierwszej wersji napisałam błędnie spójnik 'lub', chociaz na kartce miałam inaczej. Jest jeszcze w Kłaczkowie parę trudnych zadań z logarytmów. Twój sposób też by doprowadził do wyniku, obliczyć Δ, pierwiastki t₁(m) ,t₂(m) i sprawdzać warunki dla x₁(m) i x₂(m). Wiem z doświadczenia,że jeżeli popełnia się błędy, ale uparcie dąży do rozwiązania, do dobrego wyniku, to na pewno to zostaje w pamięci i w odpowiedniej chwili dostajesz sygnał ostrzegawczy w podobnej sytuacji. Ciekawa jestem, jakie to były zadania.

Mila:

	1
Z tym logarytmem to zobaczcie co napisała Eta, od razu wynik		.
	3

Piotr 10: Trudne zadania nie były na tym sprawdzianie, bynajmniej dla mnie. Robiłem o wiele trudniejsze rzeczy przed nim. Pierwsze dwa zadania to były nierówności wykładnicze i logarytmiczne, trzecie zadanie to wyznaczenie dziedziny(podchwytliwe), czwarte to obliczanie logarytmów, piąte to ta nierówność a szóste to trzeba było narysować wykres funkcji f(x)=0,5*4^x − 1, podać D⁻¹, obliczyć f[(√3−2)(√3+2)]*f(1,5), i ten parametr. Ogółem też jestem zadowolony, że podołałem w ogóle mimo, że mam teraz poważne problemy w rodzinie. Mam jeszcze jeden problem z jednym zadaniem z logarytmów, nie wychodzi mi wynik taki jak w odpowiedzi, jeśli mogłabyś sprawdzić moje rozwiązanie i podać gdzie robię błąd( na pewno czegoś nie uwzględniłem)?

Mila: Napisz. Jutro wyjaśnimy.

Piotr 10: Ok. Niedługo napiszę, tylko skończę robić inne zadanie

Piotr 10: Wyznacz wszystkie wartości parametru m, dla których nierówność log₂[m(x²+1)] ≤ log₂(4x²+4x+7) ma co najmniej jedno rozwiązanie. Założenie: D=R m>0 m(x²+1) ≤ 4x²+4x+7 (m−4)x² − 4x +m−7 ≤ 0 I przypadek, gdy m−4=0, czyli m=4 −4x ≤ 3 4x ≥ −3

	3
x ≥ −		. Jest to spełnione
	4

II przypadek, gdy (m−4)≠0 Funkcja kwadratowa ma być ''≤'' a więc Δ ≤0 Po rozwiązaniu tego otrzymuję, że m∊<3;8> Wiem, że na pewno jakiegoś warunku nie uwzględniłem. Myślałem o ramionach paraboli, czyli a >0 i a > 0

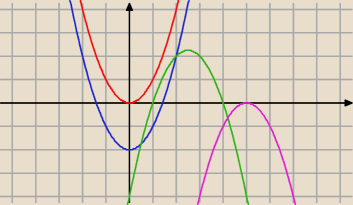
Godzio: Narysowałem wszystkie sytuacje jakie mogą być, spróbuj jeszcze raz Łatwiej to rozwiązać myśląc, kiedy to nie będzie spełnione

ZKS: Zauważ że dla m ∊ (0 ; 4) parabola jest skierowana do dołu więc tę nierówność zawsze będą spełniały jakieś liczby.

Godzio: Mam nadzieję, że się nie mylę Δ = 16 − 4(m − 4)(m − 7) = −4m² + 44m − 96

	−Δ		4m2 − 44m + 96		m2 − 11m + 24
q =		=		=
	4a		4(m − 4)		m − 4

Teza nie zachodzi gdy: a > 0 i q > 0

⎧	m − 4 > 0 ⇔ m > 4
⎩	m2 − 11m + 24m − 4 > 0	⇔ m ∊ (−∞,3) U (8,∞)

Część wspólna: m ∊ (8,∞) Bierzemy dopełnienie + m > 0 i mamy odpowiedź: m ∊ (0,8>

Piotr 10: Odp się zgadza, taka jak w odpowiedzi. Zaraz przeanalizuję to co napisałeś

ZKS: Godzio jak zawsze rozwiązanie świetne.

Eta: dla Godzia

Godzio: Rano zjem

Nie śpię bo liczę Δ: A dla mnie nie ma jabłka ? Specjalnie nie śpię, bo liczę Δ..

Eta: dla tego który, uparcie liczy i liczy....... Δ

Nie śpię bo liczę Δ: A jednak, ale to takie wymuszone

Eta: Uwaga ! jedno robaczywe zgadnij które?

Nie śpię bo liczę Δ: Oba

Mila: To już nie piszę mojego rozwiązania, jest tradycyjne.

MonicaAlexandra: Na czym polega to dopełnienie ;c Nie bardzo rozumiem dlaczego jest taki wynik końcowy... A'=Ω\A jeśli zbiorem A jest ta suma przedziałów a dopełniam zbiorem m>0 to dlaczego taki wynik powstaje? ;c

Kacper: Masz niepełny koszyk z jabłkami. Dopełnienie koszyka to liczba śliwek, która się zmieści, aby koszyk był pełny koszyk − Ω jabłka − A śliwki A'=Ω\A