tryg
Mat: Witam, czy mógłby ktoś udowodnić prawdziwość wzoru tg(α+β)= ... najlepiej nie algebraicznie a
np rysunkiem
4 paź 20:48
Mat: tg(α+β)= (sinαcosβ+sinβcosα) / (cosα cosβ − sinα sinβ) =
[(sinαcosβ+sinβcosα) / cosα cosβ] / [ (cosα cosβ − sinα sinβ) / cosα cosβ ]
= tgα+tgβ / 1 − tgαtgβ
potrafi ktoś rysunkiem / innym sposobem ?
4 paź 21:13
Mat: help
4 paź 21:25
PuRXUTM: a na kiedy potrzebujesz
może być jutro ?
4 paź 21:31
PuRXUTM: bo właśnie miałem dzisiaj ten dowód ale nie chce mi się za bardzo tego całego przepisywać
dzisiaj
4 paź 21:32
Mat: okkeee ale nie zapomnij
ehh w końcu jest piątek wieczór
4 paź 21:34
Mat: hehe pewnie studiujemy razem patrząc na to co wrzuciłeś wcześniej
4 paź 21:35
Mila:
Dlaczego chcesz innym sposobem?
4 paź 22:03
Mat: bo łatwo się robi dowód rysunkiem na sin czy cos(α+β) a tego na tg nie mogę pojąć
4 paź 22:14
Mila:
Na tg (α+β) nie robi się tak łatwo, to zresztą nie ma znaczenia, bo musisz zrozumieć
algebraiczny sposób, później będziesz miał o wiele trudniejsze wyrażenia. Nie unikaj
problemów, lecz rozwiązuj.
Czego tam nie rozumiesz?
Napisać po kolei z wyjaśnieniem?
4 paź 22:19
Mat: Dobra może sama sobie poradzę albo poczekam do jutra może pojawi się rozwiązanie o które mi
chodzi ale dzięki Mila, algebraiczny sposób jest ok i go rozumiem .
4 paź 22:23
4 paź 22:26
Mila:
Tam, Saizou nie ma tego sposobu, którego szuka Mat.
4 paź 22:43
Janek191:
Dawniej te dowody ( na sin ( α + β) , cos (α + β) , tg(α + β) ) były w II klasie
pięcioletniego technikum − patrz. ALgebra dla II klasy ... Aniela Ehrenfeucht,
Olga Stande, Stefan Straszewicz PZWS wyd. I W − wa 1968 r.
5 paź 08:39
PuRXUTM:
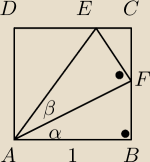
kąt DEA jest równy α+β IABI=1
| | |AD| | |
mamy wyliczyć tg( α+β )= |
| |
| | |DE| | |
| | |FB| | |
tg α= |
| czyli |FB|=tg α |
| | 1 | |
| |AB| | | 1 | |
| =cos α z tego |AF|= |
| |
| |AF| | | cos α | |
| | EF | | 1 | | tg β | |
tg β= |
| tg β * |
| =|EF| czyli |EF|= |
| |
| | AF | | cos | | cos α | |
| | |CF| | |
cos α= |
| |CF|=tg β |
| | |EF| | |
|BC|=|AD| czyli |AD|=tg α +tg β
teraz musimy wyliczyć |DE| a zrobimy to uwzględniając że |DE|=|AB|−|EC|
| | tg β | |
|EC|=sin α * |
| =tg α*tg |
| | cos α | |
|DE|=1−tg α*tg β
| | |AD| | | tg α +tg β | |
tg( α+β )= |
| = |
| c.n.d |
| | |DE| | | 1−tg α*tg β | |
PS. Studiujesz na uj ?
5 paź 10:51
pigor: ..., chyba zgrabniej dowodzi się to na płaszczyźnie w I−szej ćwiartce
z układem osi XOY i promieniem jednostkowym r=1 koła trygonometrycznego,
oraz kątem skierowanym α+β . ...
5 paź 11:30
5 paź 14:48
