równanie kwadratowe em: Dla jakich wartości parametru m dane równanie ma dwa różne pierwiastki: −mx² + 2(m − 2)x − 4m =0 wyszło mi tak: dla m = ²₃ i dla m = −2 mógłby mi ktoś to sprawdzić, proszę

Bogdan: to jeszcze nie koniec rozwiązania, dokończ i podaj swoją odpowiedź

em: a co ja mam tam jeszcze obliczyć/napisać, Bogdanie? m≠0 ?

Bogdan: Kiedy równanie kwadratowe ma dwa różne pierwiastki?

em: gdy Δ>0

Bogdan: Rozwiąż więc tę nierówność

em: powinnam podstawić m do równania delty i sprawdzić czy ta nierówność jest prawdziwa?

em: Δ = 4m² − 16m +16 = m² − 4m + 4

Bogdan: Podaj swoją deltę: Δ = ...

em: przepisałam nie to, co trzeba, poprawiam: Δ = −12m² − 16m +16

em: ! Δ = 3m² − 4m + 4 dobrze?

em: więc −3m² − 4m + 4 > 0, tak? powinnam podstawić tu te dwie wartosci m?

Bogdan: Ech. Δ > 0 ⇔ 4(m − 2)² − 16m² > 0 / : 4 (m − 2)² − 4m² > 0 (m − 2 − 2m)(m − 2 + 2m) > 0 (−m − 2)(3m − 2) > 0

	2
−3(m + 2)(m −		) > 0 dokończ rozwiązywanie tej nierówności i podaj wynik,
	3

weź pod uwagę założenie: a ≠ 0

em: −3m² − 4m + 4 > 0

Bogdan: Ech, ech aż nie chce się gadać.

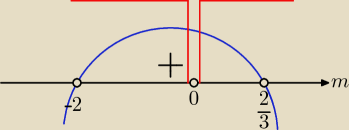
Bogdan: Skończę jednak. a ≠ 0 ⇒ −m ≠ 0 ⇒ m ≠ 0 i

	2		2
Δ = −3(m + 2)(m −		) > 0 ⇒ m ∊ (−2,		)
	3		3

	2
Odp.: Równanie ma 2 różne pierwiastki dla m ∊ (−2, 0)∪(0,		)
	3