całka potrójna aniaaaa: obliczyć całkę potrójną ∫∫∫z²√x²+y²+z² gdzie obsar U jest ograniczony poprzez nierówność 0≤z≤√4−x²−y², x≥0 , y≥0 stosuję tutuaj współrzędne sferczne? jezeli tak to wyszło mi ze r∊(0,2) z∊(0,√4−r²) ale jak wyliczyc α i β?

Krzysiek: http://pl.wikipedia.org/wiki/Uk%C5%82ad_wsp%C3%B3%C5%82rz%C4%99dnych_sferycznych#System_.22geograficzny.22 jeżeli w ten sposób przechodzisz na współrzędne sferyczne to Φ∊[0,π/2] θ∊[0,π/2] r∊[0,2] |J|=r² cosθ

aniaaaa: i tak nie rozumiem dlaczego takie przedziały θ i Φ

aniaaaa: czy mółby ktoś wytłumaczyć mi " na chłopski rozum " jak wylicza sięθ i Φ bo nie moge tego zrozumieć

Krzysiek: x≥0 i y≥0 czyli to sfera jest tylko w pierwszej ćwiartce układu współrzędnych OXY dlatego Φ∊[0,π/2] a drugi kąt jest taki bo z≥0

aniaaaa: dobra zrozumiałam tenprzykład dziękuję, a jeżeli mój obszar byłby taki: x²+y²+z²≤4x wtedy jakie byłyby granice całkowania?

aniaaaa: może ktoś pomóc?

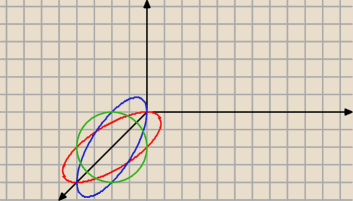
Trivial: W pierwszym przykładzie trzeba zastosować współrzędne walcowe (r,φ,z) z jakobianem r, a nie sferyczne (r,φ,θ) z jakobianem r²cosθ. Granice na r i z już masz, pozostało zastanowić się jaka będzie granica na φ. (pierwsza ćwiartka Oxy → φ∊[0,^π₂]). W drugim przykładzie, przejdź na współrzędne sferyczne (r,φ,θ) z jakobianem r²cosθ. r² ≤ 4rcosφcosθ / : r r ≤ 4cosφcosθ Granice na φ i θ odczytasz z rysunku. Ostatecznie:

	⎧	0 ≤ r ≤ 4cosφcosθ
G:	⎨	−π2 ≤ φ ≤ π2
	⎩	−π2 ≤ θ ≤ π2

aniaaaa: ok dziękuję. w takim bądź razie kiedy stosuje się współrzędne sferyczne a kiedy walcowe?