indukcja zadanie: Udowodnij, że dla każdej liczby naturalnej n≥6 kwadrat można rozciąć na n kwadratów. kwadrat mozna podzielic na 6 kwadratow T(6) ale pozniej w rozwiazniu pojawia sie T(n+3) skad bierze sie ta 3?

PW: Dzielą jeden z kwadratów na 4 kwadraty (bo na mniej nie można), stąd liczba kwadratów zwiększa się o 3.

zadanie: dziekuje

Mila: Jak Ci poszło?

zadanie: no niestety nie zdalem ale trzeba szukac pozytywnych stron moze sie wiecej naucze bo teraz musze chodzic na ten przedmiot ale po omowieniu tego testu na zajeciach zrobilem glupie bledy jak zawsze

zadanie: Posluguj¡c sie wspólczynnikami kierunkowymi uzasadnij, ze dowolny kat wpisany w okrag i oparty na jego srednicy jest katem prostym. Wskazówka: dobierz uklad wspólrzednych tak, by punkt O pokrywal sie ze srodkiem okregu, zas wyrózniona srednica byla zawarta w osi Ox mam taki rysunek:

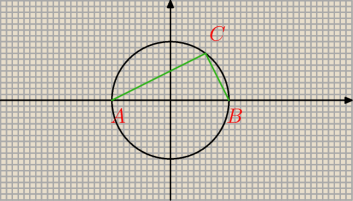
zadanie: A(x₁,0) B(x₂,0) C(x,y)

	y
kAC=
	x1+x

	y
kBC=
	x1−x

k_AC*k_BC=−1 wtedy te proste sa prostopadle czyli ten kat bedzie prosty

	y2
kAC*kBC=
	x12−x2

i co teraz ?

zadanie: 2. Rozstrzygnij czy nastepujacy punkt lezy na osi Ox czy 0y (0,0) no wlasnie on lezy i na tej osi i na tej czyli na dwoch jednoczesnie?

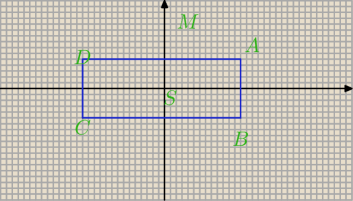
zadanie: 3. Wykaz, ze suma kwadratów odleglosci dowolnego punktu M od wierzcholków danego prostokata rózni sie od poczwórnego kwadratu odleglosci punktu M od srodka prostokata o stala wartosc liczbowa, niezalezna od polozenia punktu M. Wskazówka: dobierz uklad wspolrzednych o osiach równoleglych do boków prostokata; przyjmij niezbedne oznaczenia. A(x,y) B(x,−y) C(−x,−y) D(−x,y) S(0,0) M(M_x,M_y) suma kwadratow odleglosci dowolnego punktu M od wierzcholków danego prostokata jest rowna 4x²+4y²+4M_x²+4M_y² poczworny kwadrat odl. punktu M od srodka prostokata 4*ISMI²=4*(M_x²+4M_y²) i co dalej?

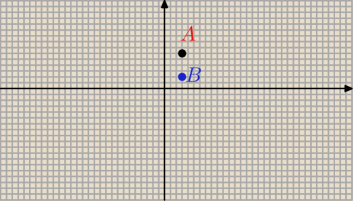
zadanie: 4. Znalezc punkt równo oddalony od obu osi wspólrzednych i od punktu (3,6). A(3,6) B(x,x) bo rowno oddalony od osi Ox i Oy IABI=x a jeszcze inaczej mozna jezeli to jest w ogole dobrze?

zadanie: prosilbym o pomoc w tych zadaniach

Mila: 4x²+4y²=(2x)²+(2y)²=d² − kwadrat długości przekątnej 4x²+4y²+4M_x²+4M_y²−4*(M_x²+M_y²)=d² − stała wielkość dla danego prostokąta

Mila: Zadanie 4. Zapisz równości odległości.

Mila: 4) |x|=|y| B(x,x) |AB|=|x|=|y| |x|=√(x−3)²+(x−6)² /² dokończ,

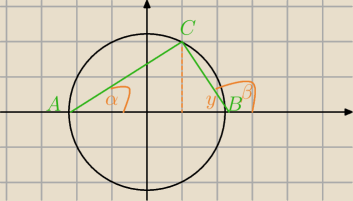
Mila: 1) C∊ I ćwiartki x²+y²=r² C(x,√r²−x²) A=(−r,0) B=(r,0)

	y		√r2−x2
kAC=tgα=		=
	x+r		x+r

	−y		−√r2−x2
kBC=tgβ=−tgγ=		=
	r−x		r−x

tgα*tgβ=−1 sprawdź,

zadanie: dziekuje

zadanie: 1.

	√r2−x2		−√r2−x2		−(r2−x2)
tgα*tgβ=		*		=		=−1
	r+x		r−x		r2−x2

zadanie: 4. x²=x²−6x+9+x²−12x+36 x²−18x+45=0 Δ=324−180=144; √Δ=12 x=3∨x=15 stad B(3,3)∨B(15,15)

zadanie: mam pytanie do 3 zadania dlaczego od sumy kwadratów odleglosci dowolnego punktu M od wierzcholków danego prostokata czyli od 4x²+4y²+4Mx²+4My² odejmujemy poczworny kwadrat odl. punktu M od srodka prostokata czyli 4Mx²+4My² ?

zadanie: i do 1. A(−r,0) B(r,0) punkt B ma wspolrzedna x−owa r bo jest to odleglosc od osi y a ta odleglosc to promien okregu czyli r tak?

Mila: Ad3. W zadaniu pisze że suma.(.. ) ..różni się od poczwórnego kwadratu (...), więc odejmując obliczamy o ile się różni. Ad1. tak.

zadanie: dziekuje a jeszcze 2 zadanie to jest os 0y czy 0x?

Mila: PUNKT przecięcia osi.

zadanie: dziekuje

Mila: Nie unikaj wykładów , które rozszerzają Twoje wiadomości. Na pewno będzie inne ujęcie materiału niz w szkole i to przyda się. Nie przejmuj się tym testem, cierpliwie pracuj, szukaj dobrej literatury, zasięgaj porady w tej sprawie u starszych kolegów.

zadanie: jeszcze nie opuscilem zadnego i mam nadzieje, ze nie opuszcze

Mila: Tak trzymaj. Powodzenia, nie zrażaj się trudnościami. Pracuj wytrwale. Nas straszyli na różne sposoby. Odporni na stres i pracowici zostali. Fakt, że selekcja była na egzaminie wstępnym, potem na I egzaminie ze wstępu do matematyki, zadania były trudne, dużo osób nie podołało.