Wyrażenia algebraiczne DeDee: Dla jakich wartości parametru m oba pierwiastki równania mx²−2(m−3)x−6(3−m)=0 zawarte są między 0 i 1?

wredulus_pospolitus: 2 > x₁+x₂ > 0 0 < x₁*x₂ <1 wzory Viete'a się kłaniają

Bizon: i sądzisz miły wredusie, że to wystarczy ? −

Bizon: ... wzory Viete'a nie "załatwiają" odpowiedzi na pytanie: − kiedy równanie jest kwadratowe ... warunek dla m − kiedy równanie ma dwa pierwiastki ... warunek dla Δ

pigor: ..., no właśnie, ja widzę to np. tak : niech

	−b
f(x)=ax2+bx+c i p=		− odcięta wierzchołka paraboli funkcji f, to,
	2a

tutaj f(x)= mx²−2(m−3)x−6(3−m), a wtedy warunki zadania spełnia koniunkcja (układ) nierówności np. taki : f(x)=0 i 0 < x₁< x₂ < 1 ⇔ ⇔ Δ >0 i af(0) < 0 i af(1) < 0 i 0 < p < 1 ⇔

	2(m−3)
⇔ 4(m−3)2−4m*6(m−3) >0 i mf(0)< 0 i mf(1)< 0 i 0<		< 1 ⇔
	2m

⇔ (m−3)²−6m(m−3)>0 i m(−18+6m)<0 i m(m−2m+6−18+6m)<0 i 0< m(m−3)<m² ⇔ ⇔ no to baw się teraz dalej sam . ...

DeDee: przy Δ nie powinno być 3(m−3)²−4m*(−6(3−m)>0?

Piotr 10: pigor a nie powinno być przypadkiem a*f(0) >0 ⋀ a*f(1) > 0 ?

DeDee: No mnie też się tak wydaje. A więc jak będzie to ostatecznie wyglądać?

DeDee: 4m²−24m+36+24m²−72m>0 28m²−96m+36>0 7m²−24m+9>0 Δ=156 dobrze to sie robi?

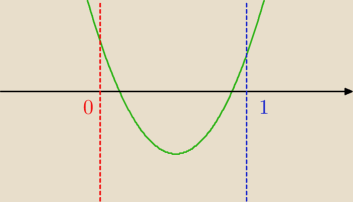
Kejt: dla a>0 pierwiastki będą zawarte między 0 i 1 dla f(1);f(0)>0 (widać na rysunku) nie jest tu pewna, czy możemy mówić o jednym pierwiastku dwukrotnym, sam podejmij decyzję.. mam nadzieję, że dobrze. (podobnie dla a<0)

ZKS: Kejt można bez rozbijania na przypadki dla a > 0 oraz a < 0. Wystarczy że zapiszemy af(0) > 0 ∧ af(1) > 0.

Kejt: jak już mówiłam w którymś poście.. za krótko spałam, więc mogę niektórych rzeczy nie zauważać Nie mniej jednak dziękuję za uwagę..

ZKS: Nie czytam wszystkich postów więc nie wiedziałem że krótko spałaś.

Kejt: spoko, nie ma sprawy miałam dziś wykłady na 7.15 => pobudka o 4.30 rano..

ZKS: To ile kilometrów od uczelni mieszkasz że tak rano musiałaś wstawać? Oj jak ja mam dobrze dzisiaj wolne miałem.

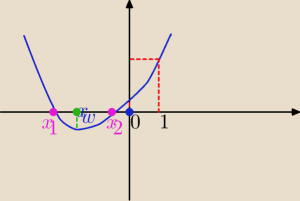
Eta: kontrprzykład

Kejt: nie aż tak daleko.. ale komunikacja miejsca pozostawia wiele do życzenia.. racja Eta.. dołożenie warunku 0<x_w<1 wystarczy?

Eta: Tak, teraz ok Pozdrawiam

pigor: ..., przepraszam kurde, no jasne tak :iloczyny >0 , bo a i f() muszą być jednakowego znaku .

Eta: pigor się "obudził"