potrzebne, pilnie. Hope: 1. Narysuj zgrubnie poprzez przesunięcie i przeskalowanie wykres funkcji. a. y= 2sin(3x−π)+4 b. y= 3x−2/4x−1 4. Dla danych punktów A(1,4) oraz B(2,3) na prostej o równaniu x+y=6 znajdź taki punkt C, że trójkąt ABC ma najmniejszy obwód. 5. Oblicz wartość 3√2+√5 + 3√2−√5

Lorak: zgrubnie? może zgrabnie?

Kostek: zgrubna to jest obróbka metalu

Hope: zgrubnie ; )

Lorak: a) y=2sin(3x−π)+4

	π
y=2sin3(x−		)+4
	3

Można np. tak: Kolejno:

	π
sinx → sin3x → 2sin3x → translacja o wektor u=[		,4]
	3

Lorak: nie znałem tego słowa, ale rzeczywiście istnieje i oznacza między innymi 'szkicowo'

Hope: i to wszystko w tym a?

Lorak: tak, wystarczy tylko narysować

Hope: b? ; D i pozostałe?

Lorak: ja muszę już lecieć. z zadaniem 5 powinieneś sobie poradzić bez problemów...

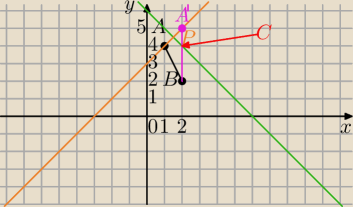
Mila: Dla danych punktów A(1,4) oraz B(2,3) na prostej o równaniu x+y=6 znajdź taki punkt C, że trójkąt ABC ma najmniejszy obwód. Suma |AC|+|BC| ma być najmniejsza k: y=−x+6 C∊K⇔C=(x,−x+6) Znajdziemy punkt A' symetryczny do A względem prostej k, leży on na prostopadłej do k i przechodzącej przez A m: y=x+b, 4=1+b, b=3 m⊥k : y=x+3 Punkt przecięcia prostych: x+3=−x+6⇔ 2x=3 x=1,5, y=4,5 P=(1,5;4,5) jest środkiem odcinka AA', A'=(x',y')

	1+x'
1,5=		⇔3=x'+1⇔x'=2
	2

	4+y'
4,5=		⇔9=4+y'⇔y'=5
	2

A'=(2,5) AP=PA' |A'C|+|BC'| najkrótsza droga z A poprzez C=(2,−2+6)=(2,4) do B.