twierdzenie Talesa, zupełnie nie wiem z której strony to ugryść Maciek: W kwadracie poprowadzono proste rownoległe do jednej z przekątnych w równych odległościach. Podzielily one kwadrat na 3 części o równych polach. Oblicz długosc boku kwadratu jezeli odcinki na prostych równoległych do przekatnej sa długosci 6 cm.

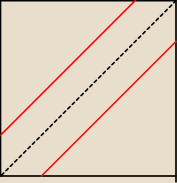
Janek191: Czerwone odcinki mają długość 6 cm. Pola trójkątów prostokątnych i pole sześciokąta są równe. a = długość boku kwadratu Mamy P_Δ = 0,5*0,5*6² = 0,25*36 = 9 Pole kwadratu P = 3 *P_Δ czyli a² = 3*9 a = √3*9 = √9*3 = 3 √3 Odp. a = 3 √3 cm ==================

czaroo: nie rozumiem z jakiego wzoru wyszło: PΔ = 0,5*0,5*62 = 0,25*36 = 9

Janek191: d − długość przekątnej kwadratu d = 6 cm Pole kwadratu P = 0,5 d² = 0,5*6² Pole trójkąta prostokątnego, którego przeciwprostokątną jest przekątna kwadratu jest równe P_Δ = 0,5 P = 0,5 *0,5 d² = 0,25*6² =0,25*36 = 9