Oblicz długość boku w 8-kącie formenym znając jego pole. zq: Oblicz długość boku ośmiokąta foremnego, jeżeli pole wynosi 3000 metrów kwadratowych. (proszę o obliczenia i możliwie prostą metodę. Z góry dziękuję!)

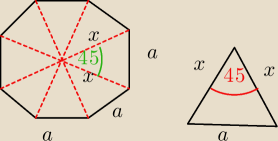
Monika: Pole ośmiokąta foremnego jest równe sumie pól ośmiu trójkątów. Kąt wewnętrzny w trójkącie wynosi 360/8 czyli 45 stopni. Pole jednego trójkąta można policzyć ze wzoru ¹₂x²*sinα, gdzie α=45 stopni Pole figury wynosi 3000m² i jest równe sumie pól trójkątów, więc: 3000 = 8*¹₂x²*sin45 3000=4x²*^√2₂ 3000=2x²*√2 x² = ¹⁵⁰⁰_√2 x²=^150√2₂ x² = 750√2 Z twierdzenia cosinusów: a² = x²+x²−2*x*x*cos45 a² = 2*750√2 − 2*750√2*^√2₂ a²=1500(√2−1) a=10√15(√2−1)

zq: Dziękuję za odpowiedź, ale nie można tego obliczyć w inny sposób? Jestem dopiero w gimnazjum i nie mam pojęcia co to ''sin'' albo ''twierdzenie cosinusów''.

Monika: sin = to jest sinus kąta Zaraz pomyślę nad innym sposobem

Monika: możesz skorzystać też z gotowego wzoru na pole ośmiokąta: P= 2a² (1+√2) bez sinusów, to ciężko cokolwiek mi zrobić.

PW: Biorąc pod uwagę dwa kolejne trójkąty narysowane przez Monikę zobaczymy deltoid, a którym jeden z kątów jest prosty (45°+45°). Pozwoli to obliczyć jego przekątną za pomocą x − z twierdzenia Pitagorasa. Pole deltoidu umiemy obliczyć za pomocą przekątnych, a więc wyznaczymy x. Przelicz to zq i zobacz, czy otrzymasz to samo co Monika

Mila: W której jesteś klasie i jaki dział teraz przerabiacie, że Pani takie zadanie Ci zadała?

zq: Mila: w II, pani bardzo lubi takie zadania, robimy to na "dodatkowej"−obowiązkowej godzinie...

zq: Więc chyba obliczę to ze wzoru. 3000 = 2a² (1+√2) i co dalej? Pomóżcie, bo już jestem zmęczona .

Mila: A nie chodzi o sześciokąt foremny? Jaki dział przerabiacie?

Mila: Teraz muszę przerwać , pracę, na pewno ktoś Ci z tego wzoru napisze. Wieczorem zerknij, może wpadnę na to, o co Pani chodziło.

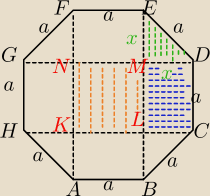
Mila: 1) P_ΔEMD: z tw. Pitagorasa x²+x²=a²⇔2x²=a² Masz 4 takie trójkąty:

	1
PΔEMD=		*x2
	2

	1
4*PΔEMD=4*		*x2=2x2=a2
	2

Pole kwadratu KLMN=a² P_▭LCDM=x*a Masz 4 takie prostokąty 4*P_▭=4*x*a

	a2		a		a√2
Musimy jednak obliczy x; 2x2=a2 ⇔x2=		⇔x=		=
	2		√2		2

	a√2
Pośmiokata=a2+a2+4*		*a=2a2+2a2√2=2a2(1+√2)
	2

P_ośmiokąta=2a²(1+√2) 2a²(1+√2)=3000 a²(1+√2}=1500 /*(√2−1) a²*(2−1)=1500*(√2−1) a²=1500*(√2−1) a=√1500*(√2−1) =10√15*(√2−1) To wg mnie przekracza zakres materiału w II GM w obecnej chwili.

zq: O, bardzo dziękuję, naprawdę : −)! Teraz robimy o dział o liczbach − potęgi, pierwiastki itp. A jeśli trzeba by obliczyć obwód jeśli pole = 3000, to też trzeba tak samo liczyć (wynik razy 8), czy jest może jakiś inny sposób?

Mila: Jest też wzór na pole wielokąta wypukłego: P=p*r, gdzie p− polowa obwodu wielokąta, r− promień okręgu wpisanego w wielokąt Jeśli miałaś podany promień, to sprawa prosta, podstawiasz do tego wzoru.

PW:

	1
Pomyśl o tym deltoidzie. Znamy jego pole		pola ośmiokąta. Z drugiej strony pole deltoidu
	4

jest równe połowie iloczynu jego przekątnych. Przekątne to x i √2x. Liczbę x wyliczymy bez

	1
kłopotu. Deltoid składa się z dwóch trójkątów − jeden prostokątny, a więc ma pole		x2.
	2

Wyliczymy zatem wysokość h opuszczoną na przeciwprostokątną. Znamy też pole drugiego trójkąta. Znamy jego podstawę √2x. Wysokość drugiego trójkąta składającego się na deltoid jest równa x−h. Jest to trójkąt o podstawie √2x, wysokości x−h i ramionach a. To pozwoli wyliczyć a.