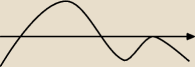
Co wynika ze wzoru ciągu? Ac.: Ciąg (a_n) określony jest wzorem a_n = −n(2−n)(3−n)². Wynika z tego, że A. a₁ > 0 B. a₂ > 0 C. a₃ > 0 D. a₄ > 0 Wiem, że mogę to zrobić, podstawiając kolejno 1, 2, 3 i 4 pod wzór, ale to rozwiązanie jest najdłuższe. Próbowałem zrobić to innym sposobem: −n(2−n)(3−n)² > 0 (wykres jest na górze, tam są przecięcia osi OX w punktach 0, 2, 3) Rozwiązaniem jest n ∊ (0, 2) (0, 2) ∩ N₊ = {1} Czyli wychodzi mi, że a₁ > 0. Tymczasem prawidłową odpowiedzią jest a₄ > 0. Co jest złego w moim rozumowaniu?

ICSP: Wykres powinien isć od góry. Przecież współczynnik przy najwyższej potędze jest dodatni

Ac.: Współczynnik przy najwyższej potędze? Mnie uczono, że patrzymy na znak przy wielomianie. Ta potęga druga przy 3−n chyba wskazuje na to, że wykres się odbija od osi OX. Tak przynajmniej też pisze na stronie 142. To teraz już w ogóle nie wiem, co robię źle.

krystek: Wymnóż sobie −n(−n)(n²)=+n³

krystek: ups n⁴

Ac.: Chodzi o to, żebym wziął sobie z każdego czynnika n ze znakiem? Czyli mam −n, −n i (−n)² i po wymnożeniu otrzymuję n⁴. I zaczynam od góry, bo przy n⁴ mam +, tak? Jeśli o to chodzi, to już wszystko rozumiem. A swoją drogą pomyślałem, że można to też zrobić tak, że wyciągam minus przed nawias i zmieniam znaki w nawiasie tak, żeby przy n był +. Czy ten sposób też byłby dobry?

krystek: Tak

Ac.: W takim razie dziękuję za pomoc.