wyznacz dziedzinę funkcji: Justa: Mam jeszcze problem z jednym zadaniem: wyznacz dziedzinę funkcji: f(x)= log_x²−3 (x²+2x+3) Z góry dziękuję

bezendu: x²−3>0 i x²−3≠1 i x²+2x+3>0

Piotr 10: x²−3 > 0 ⋀ x²−3≠1 ⋀ x²+2x+3>0 Rozwiąż to i zrób cześć wspólną tych 3 zbiorów

Justa: a dlaczego x²−3≠1 ?

Piotr 10: https://matematykaszkolna.pl/strona/217.html poczytaj

matyk: bo podstawa logarytmu nie może być równa 1

bezendu: Piotr Ty nie w szkole ?

Justa: Dziękuję

Piotr 10: Tak nie w szkole, bo mam problemy teraz poważne

Justa: w równaniu x²+2x+3>0 Δ jest ujemna, czyli nie ma wyniku?

Piotr 10: Jeżeli delta jest ujemna czyli Δ<0 i współczynnik kierunkowy a=1. Zatem wykres jest zawsze ponad osia OX i dla każdego x∊R funkcja ta będzie większa od zera

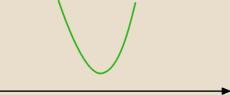
bezendu: a dla mnie x∊R

matyk: x²+2x+3>0 ⇔ x∊R

bezendu:

Piotr 10: A Ty bezendu co robisz? Też nie w szkole?

bezendu: Też nie w szkole

matyk: To tylko ja mogę powiedzieć, że nie łamię prawa

Justa: o kurde, ale mam braki mam wyliczone, że x>√3, ⋀ x≠2 ⋀ x>0 czyli x należy do (√3, +∞) \{2}, można tak zapisać?

matyk: a dlaczego x>0 skąd ten warunek?

matyk: Piotr10 napisał ci wszystkie warunki. Nie ma tam x>0

Justa: przyjęłam tak dla wszystkich liczb, bo wykres będzie taki, jak namalował Bezendu

Justa: ok, czyli ten trzeci odpada

matyk: mamy mieć sumę 2 przedziałów bez {−2,2}

Justa: a dlaczego bez −2?

Aga1.: x²−3≠1⇒x²≠4⇒(x≠2 i x≠−2)