Wyznacz zbiór wartości funkcji
immfine : Wyznacz zbiór wartości funkcji
| | 1 | | 1 | | kπ | |
f(x) = |
| + |
| ⋀ x∊R − {x: x = |
| ⋀ k∊C} |
| | cos2 x | | sin2 x | | 2 | |
2 paź 22:37
ICSP: | | 1 | | 4 | | 4 | |
f(x) = |
| = |
| = |
| |
| | sin2xcos2x | | 4sin2cos2x | | sin2(2x) | |
zatem mamy (po uwzględnieniu założeń danych w naszym zadaniu
−1 < sin2x < 1
0 < sin
2(2x) < 1
Chyba tak ,ale rozwiązania w 100% pewien nie jestem.
2 paź 22:42
Saizou : | | 1 | | 1 | | sin2x+cos2x | | 1 | |
f(x)= |
| + |
| = |
| = |
| = |
| | cos2x | | sin2x | | (sinxcosx)2 | | (sinxcosx)2 | |
no i teraz pomyśl
2 paź 22:45
immfine : | | sin2 2x | |
skąd wzięło się to |
| ? |
| | 4 | |
2 paź 22:47
Saizou : bo
sin2x=2sinxcosx
2 paź 22:48
Saizou : no i zauważmy że mianownik przyjmuje wartości (0:1), zatem gdy dzielimy przez liczbę bliską
zeru to wynik będzie wysoki (będzie w nieskończoności), a gdy dzielimy przez liczbę bliską 1
to wynik będzie bliski 4
zatem ZW=(4:+∞)
2 paź 22:51
isia:
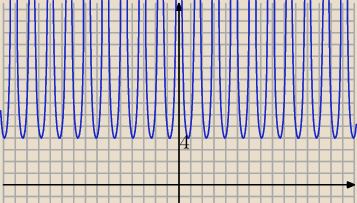
2 paź 22:52
immfine : czy zbiór nie ma być przypadkiem domknięty przy czwórce? bo sinx ≤ 1 i sinx ≥ −1
2 paź 22:57
Saizou : a zobacz co wypada z dziedziny

2 paź 22:57
immfine : ah no tak pominęłam to
2 paź 22:58
immfine : jednak dalej nie rozumiem jak to sie stało że akurat 4 wypada z dziedziny kpi/2
2 paź 23:01
immfine : zrobiłam to metodą graficzną, za to co wyszło w f(x) podstawiłam t i wyszła mi hiperbola, którą
ograniczyłam i nie wiem czemu przy czwórce ma być zbiór otwarty

tzn rozumiem że z dziedziny
ale nie wiem jak to się dzieje
2 paź 23:03
Saizou : bo nigdy nie będziemy dzielić przez 1 (bo np. dla k=1, mamy (sinπ)2=1, a to wypada z dziedziny
), zatem będziemy dzielić przez liczbę x→1 (liczba x dąży do 1, ale nigdy jej nie osiąga),
zatem nigdy też nie osiągnie się 4, tylko liczbę a→4
2 paź 23:04


 tzn rozumiem że z dziedziny
ale nie wiem jak to się dzieje
tzn rozumiem że z dziedziny
ale nie wiem jak to się dzieje