Funkcja liniowa Gabrysia : Wyznacz wartości parametru m, dla których dziedziną funkcji jest 1) f(x) = √(lml−1)x + 3 jest zbiór R 2) f(x) = ¹_{√ (m²−16)x −m} jest zbiór R

Gabrysia : umiałby ktoś to rozwiązać :C proszę o pomoc mam jutro być z tego pytana ;x

ICSP: Kiedy masz pierwiastek parzystego stopnia dajesz założenie aby liczba podpierwiastkowa była ≥ 0 Można to zapisać tak : √a to D : a ≥ 0 u ciebie : √(|m| − 1)x + 3 to dziedzina : (|m| − 1)x + 3 Teraz autor zadania "rozkazuje" ci znaleźć takie m aby dziedziną była każda liczba rzeczywista, inaczej nie ważne co wstawię pod x wartość pod pierwiastkiem ma być nie ujemna Akurat z funkcją liniową sytuacja jest bardzo prosta : √ax + b będzie miał dziedzinę daną zbiorem liczb rzeczywstistych wtedy kiedy spełnia dwa warunki : 1^o a = 0 2^o b ≥ 0

Gabrysia : f(x)= √(lml−1)x+3 ⇔ (lml−1)x+3 ≥0

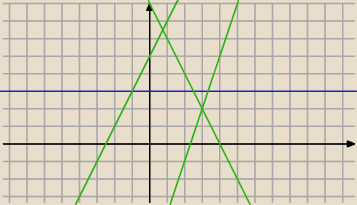
ICSP: i masz kilka wykresów funkcji liniowej. Jak widzisz tylko funkcja stała (niebieska) leży zawsze nad osią OX

Gabrysia :

⎧	lml−1=0
⎩	3≥0

⎧	lml=1
⎩	3≥0

m=1 v m=−1

Gabrysia : dobrze to zrobiłam?

ICSP: dobrze Czyli dla m = 1 v m = −1 dziedziną funkcji f(x) = √(|m| −1)x + 3 będzie zbiór liczb rzeczywistych

Gabrysia : okey to rozumiem a w tym 2 to to co mam w mianowniku musi być ≥0 a=0 i b≥0

ICSP:

1
	to dziedzina : a > 0 . Już niestety nie może być równe ( nie można dzielić przez 0)
√a

Gabrysia : czy jako dziedzinę wziąć to w mianowniku bez pierwiastka ?

Gabrysia : m²−16>0 m>0 (to trzeba pisać?) m²>16 m>4vm<−4

Gabrysia : i co teraz z tym?

ICSP: Muszą być spełnione jednocześnie dwa warunki 1^o m² − 16 = 0 2^o −m < 0 1^o m² − 16 = 0 ⇒ m = 4 v m = − 4 2^o −m > 0 ⇒ m < 0 Biorąc część wspólną 1^o oraz 2^o dostaje odp m = − 4

ICSP: 2^o −m > 0 oczywiście

Gabrysia : ej w pierwszej 2 masz −m<o a w drugiej −m >0

Gabrysia : a jak mam f(x)=√2−m−x ⇔ x∊<1, +∞) to jak to będzie

ICSP: na razie zapomnij o x ∊ <1 ; + ∞) i ustal dziedzinę funkcji : f(x) = √2 − m − x w zależności od m

Gabrysia : musi być ≥0

ICSP: 2 − m − x ≥ 0 Teraz dalej

Gabrysia : ≥1 *≥

Gabrysia : x≤2−m

ICSP: x ≤ 2 − m ⇒ x ∊ (− ∞ ; 2 − m> teraz już widać że nie istnieje takie m aby x ∊ (− ∞ ; 2 − m> był równy <1 ; + ∞)

Gabrysia : x∊(−∞;2−m> ≠x∊<1;+∞) można tak inaczej zapisać?

ICSP: ogólnie ten typ zadania sprowadza się do czegoś takiego (poprawię treść aby pasowała ) f(x) = √2 − m + x , D : x ∊ < 1 ; + ∞) Wyznaczyć takie m aby dziedziną funkcji f(x) był podany wyzej przedział. Najpierw szukamy dziedzine funckji f : D : 2 − m + x ≥ 0 ⇒ x≥ m − 2 ⇒ x ∊ < m − 2 ; + ∞) i teraz zauważamy ze aby dziedzina f(x) był podany przedział jego lewy koniec musi się zgadzać stą : m − 2 = 1 ⇒ m = 3 − dla m = 3 U ciebie na oko widać że coś jest nie tak

iejscem zerowym funkcji : no tak miałam jeszcze 2 przykłady wzorując się na tym co miałam na lekcji zrobiłam tak. DObrze? 1) f(x) = √−x+m ⇔ x∊(−∞;2> MIEJSCEM ZEROWYM FUNKCJI f y=√−x+m jest x=2 0=√−x+m 0=−x+m x=m x=2 ⇔ 2=m

iejscem zerowym funkcji : 2) f(x)= √2x−3m ⇔ x∊<6;+∞) MIEJSCEM ZEROWYM FUNKCJI f y=√2x−3m jest x=6 0=√2x−3m 0=2x−3m 2x=3m x=1,5m x=6 ⇔ 6=1,5m m=4

ICSP: wygląda dobrze

ICSP: Drugie też dobrze

iejscem zerowym funkcji : uf xd to dobrze bo się już bałam jak w tamtych przykładach mi dziedzinę kazałeś wyznaczać, żę tutaj też trzeba

ICSP: Każde zadanie można zrobić na więcej niż jeden sposób

iejscem zerowym funkcji : a jak mam przykład f(x)=¹_√m²x−8m jest przedział (4;+∞)

iejscem zerowym funkcji : to m²=0 8m>0 ?>

ICSP: a to już ciekawszy przykład 1. Ustalamy dziedzinę :

	8		8
D : m2x − 8m > 0 ⇒ m2(x −		) > 0 ⇒ m ≠ 0 oraz x −		> 0
	m		m

wiec ostatecznie

	8
m ≠ 0 ⋀ x >
	m

	8
Czyli		= 4 ⇒ m = 2. (2 ≠ 0 wiec spełnia pierwszy warunek )
	m

ICSP: Dobra ja na razie idę

iejscem zerowym funkcji : jejku troszkę trudno to z początku wyglądało ale dziękuję CI bardzo, za pomoc nie wiem co bym bez Ciebie zrobiła