Trapez Blue: Przekątne trapezu ABCD przecinają się w punkcie S. Trójkąt ABS ma pole równe 8, a trójkąt CDS ma pole równe 2. Suma podstaw tego trapezu wynosi 6. Oblicz wysokość tego trapezu.

pigor: ..., np. niech a,b,h=? − standardowe oznaczenia podstaw i wysokości trapezu, to z tw. o polach ΔΔ podobnych ABS ∼ CDS i warunków zadania

a		8
	= √		= 2 i a+b=6 ⇒ a=2k i b=k i 3k=6 ⇒ k=2 i a=4 i b=2 ,
b		2

analogicznie, jeśli h₁,h₂ − wysokości ΔABS i ΔCDS odpowiednio, to h₁ : h₂= 2 i h₁=2k i h₂=k, a stąd i z równości sumy pól : ¹₂ah₁+¹₂bh₂= 8+2 ⇔ ¹₂*4*2k+¹₂*2*k= 10 ⇔ ⇔ 4k+k= 10 ⇔ k=2 , zatem także h₁= 4 i h₂=2 , więc h=h₁+h₂= 4+2=6 − szukana długość wysokości trapezu. ...

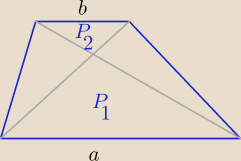isia: No to....widzę to, tak P(tr)= (√P₁+√P₂)² P(tr)= (2√2+√2)² = (3√2)²=18

	a+b
P(tr)=		*h
	2

	6
18=		*h ⇒ h= 6
	2