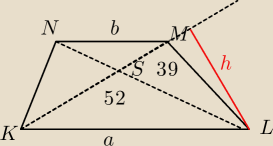
Sprawdzian, znowu.. Fasola022: W trapezie KLMN, gdzie KL jest podstawą poprowadzoni przekątne, które przecięły się w pkt S. Pola trójkątów KLS i LMS są odpowiednio równe 52 i 39. Oblicz pole trapezu. Chwilowo obliczyłam jedynie, że 1¹₃h₂= h₁ gdzie h₁−wysokość ΔKLS h₂− wys ΔLMS

Mila:

	a
ΔKLS∼ΔMNS w skali k=
	b

Stosunek pól figur podobnych jest równy kwadratowi skali podobieństwa⇔

PΔKLS
	=k2
PΔMNS

ΔKLS i ΔLMS mają taką samą wysokość opuszczoną z wierzchołka L na prostą AM

	1
PΔKLS=		*KS*h
	2

	1
PΔLMS=		*SM*h
	2

P_ΔKSN=P_ΔLMS=39

PΔKLS		1   *KS*h 2		KS		52		4
	=		=		=		=		⇔
PΔLMS		1   *SM*h 2		SM		39		3

	KS		a		4
Z podobieństwa ΔKLS i ΔMNS⇒		=		=
	SM		b		3

	4
ΔKLS∼ΔMNS w skali k=
	3

	4
PΔKLS=(		)2*PΔMNS
	3

	16
52=		* PΔMNS
	9

	9		13*9
PΔMNS=52*		=
	16		4

Dokończ

Fasola022: skąd się wzięło PΔKSN=PΔLMS=39 ?

Mila:

	1
PΔKLN=		a*H=52+x=PΔALM=52+39⇔52+x=52+39⇔x=39
	2

H− wysokość trapezu opuszczona na bok a

Fasola022: I czy według tego co wcześniej napisałaś, czyli ^Pkls_Pmns= k² to k nie powinno równać się ⁴₃², czyli ¹⁶₉

Fasola022: żle mówię, ten wynik ⁴₃powinien być spierwiastkowany chyba..?

Mila: Nie.

KS		a
	=		to jest stosunek pól Δ, które nie są podobne.
SM		b