trójkąt na płaszczyźnie Pilna: Trójkąt ABC, w którym |AC| = |BC|, A=(2,3) B=(5,4), jest równoramienny. Oblicz współrzędne C, wiedząc że wierzchołek C leży na: a) osi x b) osi y

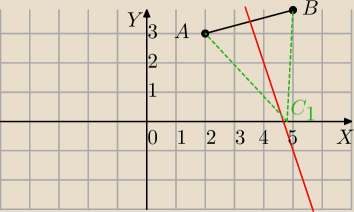
Mila: A=(2,3) B=(5,4) Wierzchołek C leży na symetralnej odcinka AB. Symetralna AB− zbiór wszystkich punktów P(x,y) jednakowo odległych od końców odcinka a i B √(x−2)²+(y−3)²=√x−5)²+(y−4)² /² x²−4x+4+y²−6y+9=x²−10x+25+y²−8y+16 ⇔ y=−3x+14 a) punkty na osi OX : (x,0)

	14		14
−3x+14=0 ⇔−3x=−14 ⇔x=		⇔ C1=(		,0)
	3		3

b) C na osi OY: (0,y)⇔ y=−3*0+14=14 C₂=(0,14)