Nierówność wykładnicza smutna: 5^2x+1 ≤ 5^x + 4 podstawiłam zmienną t i poszłam do: t ∊<−4/5;1> co dalej? może ktoś rozwiązać i powiedzieć co dalej

smutna: Prosze o pomoc

Bizon: 5t²−t−4≤0 dla t>0 ... skoryguj więc ten przedział −

Pawel.B: 5^2x+1 − 5^x − 4 ≤ 0 5^x = t i jedziesz

smutna: bizon czyli t∊(0;1>

Bizon: dokładnie

Bizon: ... i jeszcze x

smutna: o to jak bd z 5^x > 0?

smutna:

ZKS: Czy wyrażenie 5^x może przyjmować wartości ujemne?

smutna: nie

ZKS: Tak więc dla jakich x spełniona jest nierówność 5^x > 0?

smutna: nie ma takiego x

smutna: tzn jakie jest rozwiązanie? x=0 tylko?

smutna: sorki R spełnia

ZKS: Przecież teraz przeczysz sama sobie. Jaki zbiór wartości ma funkcja y = 5^x?

ZKS: Ostatnia odpowiedź jest .

smutna: czyli rozwiązanie całej nierówności jest R?

ZKS: Jak wygląda rozwiązanie dla zmiennej t?

smutna: czy część wspólna i rozwiązanie całej nierówności to : x∊(−∞; 0>

smutna: t ∊(0;1>

ZKS: Tak część wspólna i zbiór który podałaś jest .

smutna: Dzięki, głupia nierówność, niby prosta a ile kłopotów..

ZKS: Zrobisz kilka takich przykładów i już nie będzie zapewne takich kłopotów. Na zdrowie.

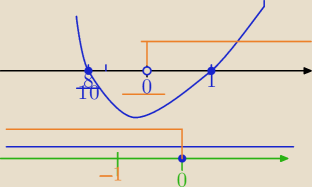
Mila: 5^2x+1 ≤ 5^x + 4⇔ 5^2x*5≤5^x + 4 t=5^x, t>0 5t²−t−4≤0 Δ=1−4*5*(−4)=81

	1−9		1+9
t=		lub t=
	2*5		10

	−8
t=		lub t=1 i t>0
	10

t∊(0,1)⇔ 0<5^x≤1 0<5^x≤5⁰ 5^x>0 dla x∊R, 5^x≤5⁰ dla x≤0 odp.x≤0

smutna: Dziekuje Mila Właśnie dokładnie tak samo zrobiłam

Mila: