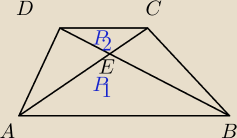
pole trojkata Hope: punkt e jest punktem przeciecia przekatnych trapezu abcd gdzie ab ∥ dc. Pola trojkatow ABE i CDE są odpowiednio równe P₁ i P₂. Niech P oznacza pole trapezu ABCD. Wykaż, że P= (√P₁ + √P₂)²

Hope: ..

Hope: ....

Mila: AB=a DC=b

	b
ΔDCE∼ΔABE w skali k=
	a

Stosunek pól figur podobnych jest równy kwadratowi skali podobieństwa.

PΔDCE		P2		b
	=		=(		)2
PΔABE		P1		a

	b		√P2
k=		=
	a		√P1

	√P2
PCEB=PΔADE=k*P1=		*P1=usuwam niewymierność z mianownika
	√P1

	√P2 *√P1 *P1
=		=√P2 *√P1
	P1

P_trapezu=P₁+P₂+2*√P₂ *√P₁=(√P₁+√P₂)²

Hope: PCEB=PΔADE=k*P1 mogłabyś wyjaśnić dlaczego te pola są sobie równe i równe k*P1 ?

Mila: 1)

	1
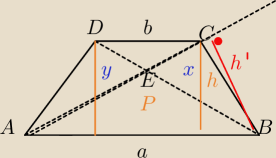
PΔABC=		a*h=P+x
	2

	1
PΔABD=		a*h=P+y⇔
	2

P+x=P+y⇔x=y 2)ΔCEB i ΔBEA maja taką samą wysokość opuszczoną z wierzchołka B na prostą AC.

CE		b		b
	=		z podobieństwa ΔDCE i ABE⇔CE=AE*		=AE*k
AE		a		a

	1
PΔAEB=		*AE*h'
	2

	1		1
PΔCEB=		*CE*h'=		*AE*k*h'=k*P
	2		2