Pomóżcie nie wiem jak to rozwiązać / funkcje Lili9: 1. Narysuj przez przesunięcie i przeskalowanie wykres funkcji ; a) y=2sin ( 3x− π) +4

	3x − 2
b) y=
	4x − 1

2. Rozwiąż nierówność : a) 4|x−2|+|3x−1| < 2|x|−3 b) √x−3 < x² −7

Basia: a wiesz jak narysować wykres y=sin3x ? od tego trzeba zacząć

Lili9: No właśnie nie wiem

Lili9: Ale jak to obliczyć, żeby taki wykres wyszedł ? Ja nigdy nie miałam tego typu funkcji...

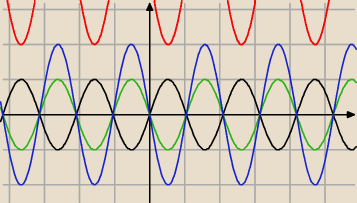
Basia: zastanówmy się wobec tego jakie będą miejsca zerowe tej funkcji

	π
sin(3x) = 0 ⇔ 3x = kπ ⇔ x = k*
	3

	π
miejscem zerowym jest każda wielokrotność liczby
	3

czyli wyjdzie tak "ściśnięty" sinus (czarne) teraz rysujemy g(x) = sin(3x−π) czyli przesuwamy o π w prawo (zielone) teraz h(x) = 2sin(3x−π) czyli wszędzie podwajamy wartości (niebieskie) a teraz przesuwamy o 4 jednostki do góry (czerwone, ale zmieścił się już tylko kawałek) musisz sama dokończyć, ten ostatni krok jest prosty

Lili9: To wszystko ? Dzięki A możecie mi powiedzieć czy to jest na poziomie rozszerzonym ? I pomóżcie w pozostałych przykładach bo tego nie rozumie

Basia: tak; takie zadania rozwiązuje się na poziomie rozszerzonym

Lili9: A mogłabyś mi pomóc w pozostałych przykładach ? Byłabym bardzo wdzięczna

Basia: 1.b

	3x−2		34(4x − 83)
f(x) =		=		=
	4x−1		4x−1

3		4x − 1 − 53
	*		=
4		4x−1

3		4x−1		53
	*[		−		] =
4		4x−1		4x−1

3		5		1
	* [ 1 −		*		] =
4		3		4x−1

3		5		1
	−		*		=
4		4		4x−1

	5		1		3
−		*		+		=
	4		4x−1		4

	5		1		1		3
−		*		*		+		=
	4		4		x−14		4

	5		1		3
−		*		+
	16		x−14		4

	1
1. rysujesz wykres g(x) =
	x

	1		1
2. przesuwasz o		jednostki w prawo i masz h(x) =
	4		x−14

	5		5		1
3. mnożysz wartości przez −		(czyli skalujesz) i masz m(x) = −		*
	16		16		x−14

	3
4. przesuwasz o		jednostki do góry i masz f(x)
	4

o ile się gdzieś w rachunkach nie pomyliłam

Lili9: Ok dzięki Obliczenia to sobie sprawdzę, a co z drugim zadaniem ?

Basia: można było szybciej

3x−2		3(x−23)
	=		=
4x−1		4(x−14)

3		x−812
	*		=
4		x−312

3		x−312 − 512
	*		=
4		x−312

3		x−312		5		1
	*[		−		*		=
4		x−312		12		x−14

	5		1		3
−		*		+
	16		x−14		4

rysowanie tak samo, bo to samo wyszło

Basia: napisz jeszcze raz; na razie pierwszy przykład to dla mojej wygody i Twojego bezpieczeństwa, bo jak "latam" po tej stronie z góry na dół i z powrotem strasznie się mylę

Lili9: Rozwiąż nierówność : a) 4|x−2|+|3x−1| < 2|x|−3

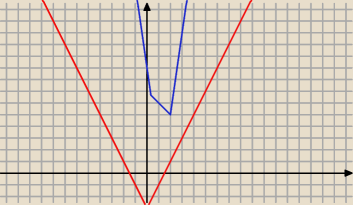
Basia: wyznaczasz i porządkujesz miejsca zerowe wyrażeń "objętych" |...| x−2 = 0 ⇔ x=2 3x−1 = 0 ⇔ x=¹₃ x = 0 czyli mamy: 0; ¹₃; 2 rozpatrujemy niestety aż cztery przedziały 1. x∊(−∞;0) ⇒ x−2<0 i 3x−1<0 i x<0 ⇒ |x−2| = 2−x i |3x−1| = 1−3x i |x| = −x i mamy nierówność 4(2−x)+(1−3x) < 2(−x)−3 8 − 4x + 1 − 3x < −2x − 3 −5x < −12

	12
x >
	5

x∊(−∞;0)∩(¹²₅;+∞) = ∅ w tym przedziale nie ma rozwiązania 2. x∊<0; ¹₃) ⇒ x−2<0 i 3x−1<0 i x≥0 ⇒ |x−2| = 2−x i |3x−1| = 1−3x i |x| = x i mamy nierówność 4(2−x)+(1−3x) < 2x−3 8 − 4x + 1 − 3x < 2x −3 −9x < −12

	12		4
x >		=
	9		3

x∊<0;^{1}[3})∩(u{4}₃;+∞) = ∅ w tym przedziale też nie ma rozwiązania 3. x∊<¹₃;2) ⇒ x−2<0 i 3x−1≥0 i x≥0 ⇒ |x−2| = 2−x i |3x−1| = 3x−1 i |x| = x i mamy nierówność 4(2−x)+3x−1 < 2x−3 8 − 4x + 3x − 1 <2x − 3 −3x < −10

	10
x >		= 313
	3

x∊ <¹₃;2)∩(3¹₃; +∞) = ∅ tu też nie ma rozwiązania 4. x∊<2;+∞) ⇒ x−2≥0 i 3x−1≥0 i x≥0 ⇒ |x−2| = x−2 i |3x−1|=3x−1 i |x| = x mamy 4(x−2)+3x−1 < 2x−3 4x − 8 + 3x −1 < 2x−3 5x < 6 x < ⁶₅ x∊<2;+∞)∩(−∞;⁶₅) = ∅ tu też nie ma rozwiązania nierówność sprzeczna; nie ma rozwiązania co widać również na wykresie niebieskie to f(x) = 4|x−2|+|3x−1| czerwone to g(x) = 2|x| − 3

Lili9: Ok to jeszcze to jak byś mogła b) √x−3 < x2 −7

matyk: Tutaj najpierw dziedzina

matyk: Potem jeśli prawa strona jest ujemna to nie mamy nic do roboty (brak rozwiązań) Jeśli prawa strona jest nieujemna, to podnosimy do kwadratu i mamy nierówność kwadratową. Na koniec zbieramy wszystko

Basia: 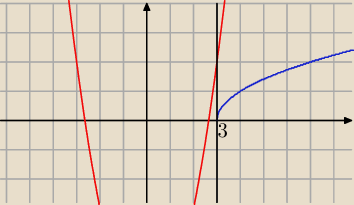√x−3 < x² −7 myślę, że tylko graficznie możesz to rozwiązać x−3 ≥ 0 x ≥ 3 a w przedziale <3;+∞) jak widać √x−3 jest cały czas < x²−7 czyli zbiorem rozwiązań jest <3;+∞)

Lili9: Ok dzięki wielkie. A jeszcze mam pytanie co do takiego zadania: Oblicz wartość : ³√2+√5 + ³√2−√5

Basia: dla x∊<3;+∞) obie strony są nieujemne, ale nierówność wychodzi koszmarna algebraicznie uczeń szkoły średniej raczej jej nie rozwiąże x−3 < x⁴ − 14x² + 49 x⁴ − 14x² −x + 52 > 0 nie warto szukać pierwiastków wymiernych bo ich nie ma; więcej: w ogóle nie ma pierwiastków

matyk: Nie zauważyłem tego kwadratu przy x² To rzeczywiście komplikuje moją metodę

Basia: nie mam już teraz czasu, ale powinien jakoś zadziałać wzór a³+b³ = (a+b)(a²−ab+b²)

	a3+b3
a+b =
	a2 − ab + b2

ale co tam wyjdzie nie wiem

Lili9: Aha. Ale dziękuje bo i tak mi dużo pomogłaś

Basia: @matyk tak samo zaczęłam; doszłam do tej nierówności i zrezygnowałam wykres pokazał, że słusznie