Wierzcholki trojkata ABC maja wspolrzedne A(1,1) B(−2,7) C(−3,−1)
Nutez: Wierzcholki trojkata ABC maja wspolrzedne A(1,1) B(−2,7) C(−3,−1)
Oblicz Pole Trojąta oraz Pole Kola opisanego na tym trojkacie
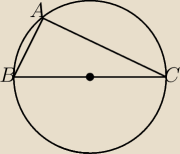
Wiec jak narysowalem to widze trojkat prostokatny , obliczam dlugość bokow i licze i za nic nie
chce wyjśc Pole: 15
licze ze wzoru na dlugosc wektora boki
2 paź 09:19
Bogdan:
|AB|
2 = 36 + 9 = 45, |AC|
2 = 16 + 4 = 20, |BC| = 64 + 1 = 65,
|AB|
2 + |AC|
2 = |BC|
2 ⇒ AB ⊥ AC
| | √45 * √20 | |
Pole P = |
| = ..., |
| | 2 | |
| | |BC| | |
Długość promienia okręgu opisanego R = |
| |
| | 2 | |
2 paź 09:30
Bogdan:
Poprawa drobna: |BC|2 = 65
2 paź 09:31
Janek191:
Np.
→
AB = [ − 2 − 1; 7 − 1] = [ − 3; 6]
→
AC = [ − 3 − 1 ; − 1 − 1] = [ − 4; − 2]
Pole
P = o,5 *det [ AB, AC ] = 0,5 *[ − 3*(−2) − 6*(−4)] = 0,5*30 = 15
================================================
I AB I = √ (−3)2 + 62 = √ 45 = √9*5 = 3 √5
I ACI = √ (−4)2 = (−2)2 = √20 = √4*5 = 2 √5
I BC I = √ ( − 3 − (−2))2 + (− 1 − 7)2 = √1 + 64 = √65
IABI2 + I ACI2 = 45 + 20 = 65 = I BC I2
Trójkąt jest prostokątny.
II sposób − obliczanie pola
P = 0,5 *I AB I* I AC I = 0,5 *3 √5* 2√5 = 3*5 = 15
=========================================
r − promień koła opisanego na trójkącie prostokątnym
r = 0,5 *c = 0,5 *I BC I = 0,5*√65
−−−−−−−−−−−−−−−−−−−−−−−−−−−
r2 = [ 0,5*√65]2 = 0,25*65 = 16,25
Pole koła opisanego na tym trójkącie
P = π r2 = 16,25*π
================
2 paź 10:34
 |AB|2 = 36 + 9 = 45, |AC|2 = 16 + 4 = 20, |BC| = 64 + 1 = 65,
|AB|2 + |AC|2 = |BC|2 ⇒ AB ⊥ AC
|AB|2 = 36 + 9 = 45, |AC|2 = 16 + 4 = 20, |BC| = 64 + 1 = 65,
|AB|2 + |AC|2 = |BC|2 ⇒ AB ⊥ AC