Równania i nierówności z wartością bezwzględną EMPE: Naszkicuj wykres funkcji f(x) = |x + 4| − |1 − x|. Na podstawie wykresu: a) wyznacz parametr m, dla którego rozwiązaniem równania f(x) = 1 − 2m jest liczba −2 b) wyznacz wszystkie wartości parametru m, dla których równanie |x + 4| − |1 − x| = 1 − 2m ma tylko jedno rozwiązanie.

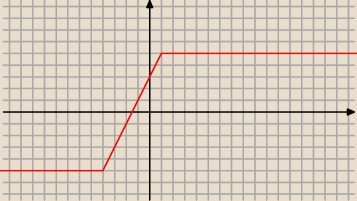
Basia: f(x) = |x+4| − |x−1| bo |1−x| = |−(−1+x)| = |−1+x| = |x−1| x∊(−∞; −4) masz f(x) = −(x+4) − [−(x−1)] = −x−4 + x −1 = −5 x∊<−4;1) masz f(x) = x+4 −[ −(x−1) ] = x+4+x−1 = 2x−3 x∊<1;+∞) masz f(x) = x+4−(x−1) = 5 naszkicuj sobie wykres tej funkcji ad.a −2 ∊ <−4;1) czyli f(−2) = 2*(−2)−3 = −7 1−2m = −7 8 = 2m m = 4 ad.b widać z wykresu; dla m∊(−5;5)

EMPE: No właśnie mnie wychodzi identycznie, tylko że w odpowiedziach do zadań mam, że: m = 1, m ∊ (−2 ; 3)

Basia: zgadza się; źle to zrozumiałam przecież |−2+4|−|1−(−2)| = 1−2m |2|−|3| = 1−2m −1 = 1 − 2m 2m = 2 m=1 natomiast (b) napisałam źle, bo się zagalopowałam 1−2m ∊ (−5;5) 1−2m>−5 6 > 2m m<3 i 1−2m<5 −4 < 2m m>−2 m∊(−2;3)

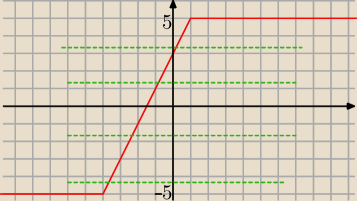
isia: a) dla x= −2 |−2+4|− |1+2|= 1−2m 2−3 =1−2m 2m=2 m=1 b) −5<1−2m<5 ⇒ 2m−1<5 i 2m−1> −5 m <3 i m > −2 m€ (−2,3)

isia: