graniastosłupy biedroneczka: proszę o pomoc.. w ostrosłupie prawidłowym czworokątnym kąt dwusieczny między sąsiednimi ścianami bocznymi ma miarę 120. oblicz miarę kata dwusiecznego między: a) ścianą boczną i podstawą b) dwiema przeciwległymi ścianami bocznymi

biedroneczka: ktos umie to zrobić?

Mila: Popraw treść.

biedroneczka: w ostrosłupie prawidłowym czworokątnym kąt dwuścienny między sąsiednimi ścianami bocznymi ma miarę 120. oblicz miarę kata dwusiecznego między: a) ścianą boczną i podstawą b) dwiema przeciwległymi ścianami bocznymi

matyk: kąta dwusiecznego?

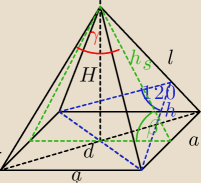
dero2005: d² = 2h²(1−cos120^o) tw cosinusów (a√2)² = 2h²(1+¹₂)

	2
h2 =		a2
	3

______________________

	hs*a
h*l = a*hs ⇒ l =
	h

	a2
hs2 = l2 −		wstawiamy za l
	4

	hs2*a2		a2
hs2 =		−		wstawiamy za h2
	h2		4

	hs2*a2*3		a2
hs2 =		−
	2a2		4

−−−−−−−−−−−−−−−−−−−−−−−−−−−−− a = h_s√2

a   2
	= cosβ
hs

hs√2   2
	= cosβ
hs

cosβ = ^√2₂ _________________ a² = 2h_s² − 2h_s²cosγ cosγ = 0

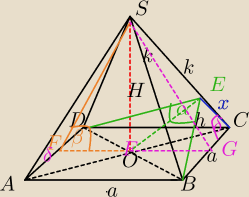Mila: α=120^o Oblicz miarę kąta dwuściennego między: a) ścianą boczną i podstawą b) dwiema przeciwległymi ścianami bocznymi. ∡OEB=60^o |AC|=a√2 − przekątna kwadratu

	1
|OB|=		a√2
	2

	OB
w ΔEOB: sin60=
	h

√3		0,5a√2
	=		⇔
2		h

	a√6
h=
	3

	OE
ctg60=
	OB

√3		OE
	=
3		0,5a√2

	√3
OE=		*a*0,5√2
	3

	a√6
OE=
	6

	a√6
x2+h2=a2⇔x2+(		)2=a2
	3

	6
x2=a2−a2*
	9

	a√3
x=
	3

	h		a√6		a√3
tgδ=		=		:
	x		3		3

tgδ=√2 W ΔSFA:

	SF
tgδ=		=√2⇔SF=U{a√2{2}
	0,5a

	OF
W ΔSFO: cosβ=
	SF

	0,5a		√2
cosβ=		=
	0,5a√2		2

β=45⁰ kąt ścianą boczną i podstawą ∡FSG=90⁰ Nie wiem, czy nie pomyliłam się w rachunkach.

Mila: Może nie, wynik jak u Dero. Pozdrawiam.