Parametr Piotr 10: Dla jakich wartości parametru m∊R równanie (m−3)*4^IxI −2m+1=0 ma dwa różne rozwiązania? Od czego to zacząć ?

Mila: Wczorajsze dokończyłeś?

Piotr 10: Jeszcze właśnie nie dokończyłem. Mam właśnie te zadania od pani profesor ze szkoły, to ok policzę tamto wcześniejsze zadanie wpierw

Basia: (m−3)*4^|x| = 2m−1 1. m−3 = 0 ⇔ m=3 0*4^|x| = 6−1 0=5 sprzeczność dla m=3 nie ma rozwiązania 2. m≠3 można podzielić przez m−3

	2m−1
4|x| =
	m−3

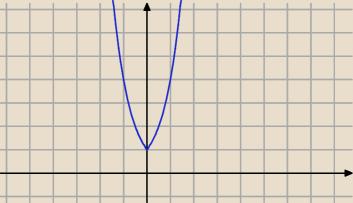
a funkcja f(x)= 4^|x| przyjmuje wartości <1;+∞) najprościej narysować wykres f(x) = 4^|x|

	2m−1
dwa rozwiązania będą ⇔		> 1
	m−3

dalej już sobie poradzisz

matyk: wyznacz ile dokładnie wynosi x i potem zastanawiaj się kiedy będą 2 te rozwiązania. Pamiętaj, że m≠3

Mila: m−3 ≠0

Piotr 10: Ok dziękuję za pomoc . Wyszło mi, że m∊(−∞;−2)∪(3+∞)

Mila: Pan Wolfram zgadza się z Tobą.

naukowikec: "najprościej narysować wykres f(x) = 4|x|" mam pytanie, trzeba rysować wykres do tego? i wgl o co chodzi z tym "funkcja f(x)= 4|x| przyjmuje wartości <1;+∞)". mógłby mi ktoś to po kolei dokłądnie wytłumaczyć?