Zilustruj zbiór wszystkich punktów płaszczyzny Ala: Zilustruj zbiór wszystkich punktów płaszczyzny, których współrzędne (x,y) spełniają równanie: |2x| = |x−2+y|

Basia: 2x = x−2+y lub 2x = −(x−2+y) przekształcić do postaci równania prostej i narysować

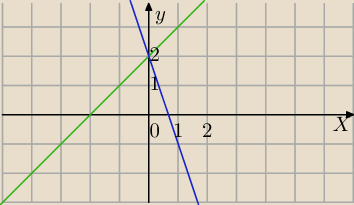
Mila: x−2+y=2x lub x−2+y=−2x⇔ y=x+2 lub y=−3x+2 suma prostych

Ala: dziękuję a jak zrobić w przypadku, gdy nie wszystko jest pod wartością bezwzględną? np. 2|x|−|y+2|=1

Gustlik: Wskazówka: Musisz zrobić tak: 1) 2x−(y+2)=1, gdy x≥0 i y≥−2 2) 2x−(−y−2)=1, gdy x≥0 i y<−2 3) −2x−(y+2)=1, gdy x<0 i y≥−2 4) −2x−(−y−2)=1, gdy x<0 i y<−2 Przekształć każde z równań do postaci kierunkowej (funkcja liniowa) i narysuj fragmenty każdej z prostych z uwzględnieniem odpowiednich założeń. Jak najprościej rysować wykresy funkcji liniowej (metoda "schodkowa" − można bez tabelki): https://matematykaszkolna.pl/forum/forum.py?komentarzdo=41 .

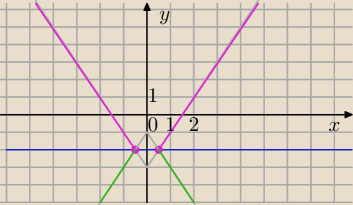
Mila: Rozważymy dwa przypadki: 2|x|−1=|y+2| 1) |y+2|=y+2 dla y≥−2 ( punkty nad prostą y=−2) y+2=2|x|−1⇔ y=2|x|−3 2)|y+2|=−y−2 dla y<−2 −y−2=2|x|−1 −y=2|x|+1 y=−2|x|−1

Ala: Ok, to też już jasne Mam problem jeszcze z jednym zadaniem. Rozwiąż algebraicznie lub graficznie układ równań: |x−y| − y= 2 x − 3y = 6

krystek: Ja tak zaproponuję dla x<y −x+y−y=2 x−3y=6 __________ dla x>y x−y−y=2 x−3y=6 ________