Funkcja Kostek: Wyznacz zbiór wartości funkcji f:N→C określonej wzorem

	n		n+1
f(n)=(−1)n*		& (−1)n*
	2		2

Basia: a co oznacza & ?

Kostek: Jeszcze raz zapiszę bo widzę że ucięło Wyznacz zbiór wartości funkcji f:N→C określonej wzorem

	n
f(n)=(−1)n*		gdy n jest liczbą parzystą
	2

	n+1
f(n)=(−1)2*		gdu n jest liczbą nieparzystą
	2

Basia:

	n		2k
n = 2k k∊C+∪{0} ⇒ (−1)n = 1 ⇒ f(n) =		=		= k
	2		2

czyli dla n parzystych otrzymamy wszystkie liczby całkowite nieujemne

	n+1		2k+1+1
n = 2k+1 k∊C+∪{0} ⇒ (−1)n = −1 ⇒ f(n) = −		= −		=
	2		2

	2k+2
−		= −(k+1)
	2

a to daje wszystkie liczby całkowite ujemne odp: ZW = C

Kostek: Też tak myślałem tylko ja rysowałem ten wykres, a jednak dało się bez rysowania

Basia:

Kostek: Wykres funkcji f(x)=x³+3x+1 przekształcono w symetrii względem prostej x=2 znajdź wzór funkcji g(x) Nie bardzo rozumiem względem prostej x=2 ? Mógłby ktoś krok po kroku wytłumaczyć to przekształcenie ?

jakubs: A to przekształcenie analogiczne jak np. względem osi OX? Czy może się mylę?

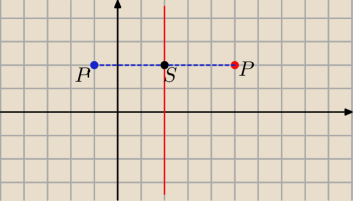Basia: x=2 czyli leżą na niej punkty o odciętej = 2 i dowolnej rzędnej czyli prosta prostopadła do OX i przechodząca przez (2,0) zastanówmy się teraz jaki jest związek między punktami symetrycznymi względem niej jeżeli P(x;y) ⇒ S(2;y) P'(x';y') PS^→ = SP'→ [2−x; y−y] = [x'−2; y'−y] 2−x = x'−2 −x = x'−4 x = 4−x' y'−y = 0 y = y' podstawiamy za x i y do równania krzywej y = x³+3x+1 y' = (4−x')²+3(4−x')+1 "prim" już można opuścić i mamy y = 64 − 3*16*x + 3*4*x² − x³ + 12 − 3x + 1 y = −x³ + 12x² − 51x + 65 i to jest wzór szukanej funkcji