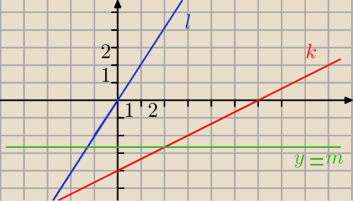
Funkcja liniowa olkaq: Cześć mam takie zadanie i nie potrafię sobie z nim poradzić: Dane są proste k i l o równaniach k: 2x − 3y −12 = 0 oraz l: 2x − y = 0 ( patrz rysunek ) Prosta o równaniu y = m gdzie (m ≠ − 6) przecina proste k i l w punktach P i Q. a) Napisz wzór funkcji, która każdej liczbie rzeczywistej m ∊ R / {− 6} przyporządkowuje długość odcinka PQ. b) Oblicz współrzędne końców odcinka PQ, jeśli |PQ| = 4.

Tadeusz: ... do równań prostych podstaw kolejno y=m Otrzymasz współrzędne punktów P i Q ... dalej chyba banał −

THIRTEEN_[13]: Dzięki

Piotruś: Czy ktoś mógłby zrobić to zadanie? Proszę o pomoc.

Piotruś:

Ala: podstawiamy m=y i mamy 2x−m=0 i 2x−3m−12=0 odejmójemy od siebie rzeby wykasowac X 2x−m−2x+3m+12=0 czyli 2m+12=0 stond m−6=0

Ala: b) m−6=0 podstawiamy dlugosc=4 4−6=−2, podstawiamy m=−2 l(m=−2) i y=m=−2 mamy 2x−m=0 , 2x−(−2)=0, 2x=2, x=1 (dla odcinka l) czyli wspolrzedne 1 punktu (x=1,m=y=−2/) to jest A(1,−2)