Na boku BC trójkąta równobocznego ABC wybrano punkt M taki, że BM= 1/3 MC. Wykaż GOGA: Na boku BC trójkąta równobocznego ABC wybrano punkt M taki, że BM= 1/3 MC. Wykaż ,że sinus kąta CAM jest równy 3√39/26. (ułamek)

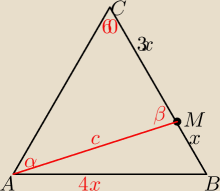
Basia: BM = x

	1
x =		MC
	3

MC = 3x to bok trójkąta ma długość x+3x = 4x z tw.cosinusów w tr.ABM c² = x²+(4x)²− 2x*4x*cos60 c² = x²+16x² − 8x²*¹₂ c² = x²+16x²−4x² = 13x² c = x√13 z.tw.sinusów w tr.AMC

c		3x
	=
sin60		sinα

c*sinα = 3x*sin60

	3x*sin60		√3   3x*   2		3√3
sin60 =		=		=		=
	c		x√13		2√13

3√3*√13		3√39
	=
2*13		26

tak się to robi i następne zadania (bo to już chyba trzecie) zacznij wreszcie liczyć sama

GOGA: no jak mi nie wychodzi i nie umiem to cikawe jak

Basia: przeanalizuj rozwiązanie i próbuj podobnego podejścia zaczynaj, próbuj, rób błędy, poprawiaj, pisz jak liczysz to ktoś poprawi na tym polega nauka; nie na przepisywaniu

Szymi: 3 linijka od dołu, jest błąd, że napisałeś/ aś sin60 =, zamiast tego powinno być sin a=

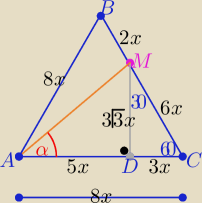
Eta: Wykopałeś zadanie sprzed 3lat Rozwiążę je tak :

	|BM|		1		2x
|∡CAM|=α i z treści zadania :		=		=		, x>0
	|MC|		3		6x

z trójkąta DMC "ekierki" o kątach 30^o,60^o,90^o |DM|=3√3x , |DB|=3x i |AB|=8x i |AD|=5x to |AM|=√25x²+27x²= 2√13x

	3√3x		3√39
zatem sinα=		= ........... =
	2√13x		26