Zapisz za pomocą przedziału lub sumy przedziałów zbiór
Sympleks: F={x: x≤3 i x<6} według mnie powinien być zbiór (−∞;6) lecz w książce Kiełbasy jest odp (−∞;3>
byłbym bardzo wdzięczny gdyby ktoś mi wytłumaczył dlaczego moja odpowiedź jest niepoprawna
30 wrz 17:19
matyk: W książce odpowiedź jest poprawna. Narysuj oś liczbową. Zauważ, że 5 nie spełnia obu
nierówności jednocześnie, a u ciebie jest w rozwiązaniu.
30 wrz 17:20
matyk:
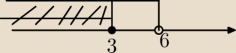
30 wrz 17:24
Mila:
Spójnik "i" oznacza część wspólną.⇔x∊(−∞,3>
30 wrz 17:28
Sympleks: Nie twierdzę, że odp książkowa jest niepoprawna
chodziło mi dlaczego MOJA odpowiedź jest niepoprawna, a nie odpowiedź z książki
Mam wyznaczyć zbiór w którym x jest mniejszy/równy 3 i mniejszy od 6 czyli według mnie jest to
zbiór który zawiera liczby od −
∞[wyłączając ją oczywiście

] do 6 (wyłączając również 6)
nie rozumiem dlaczego odpowiedzią w książce jest zbiór (−
∞;3>, dlaczego przedział (3;6) nie
należy do tego zbioru
Bardzo ale to bardzo byłbym wdzięczny gdyby ktoś mi to wytłumaczył
30 wrz 17:33
Sympleks: Ok, dziękuję Mila już rozumiem

30 wrz 17:35
Basia:
x≤3 i x<6 ⇔ (słowami) (x jest mniejsze lub równe 3) i (x jest mniejsze od 6)
weźmy liczbę 4;
4 jest mniejsze od 6, ale 4 nie jest ani mniejsze od 3, ani równe 3
liczba 4 spełnia warunek (2), ale nie spełnia warunku (1)
tak samo będzie z liczbami: 5; 5,2; 3,5; 3,1; 3,01 itd
a teraz weźmy liczbę 3
3 ≤ 3 (bo po prostu jest równe 3) i 3<6
weźmy liczbę 2
2≤3 (bo 2<3) i 2<6
te liczby spełniają i warunek (1), i warunek (2)
no to zastanów się teraz które liczby spełniają oba warunki podane w zadaniu
30 wrz 17:43
Aga1.:

Część wspólna, tam gdzie powstała kratka.Jeśli jest spójnik i, to wyznaczasz część wspólną, a
jeśli spójnik lub wówczas wyznaczasz sumę.
Liczba należy do części wspólnej, jeśli należy do obu zbiorów jednocześnie.
x≤3, czyli x∊(−
∞,3>
x<6, czyli x∊(−
∞,6)
I teraz np. 5 należy do pierwszego przedziału?Nie, więc nie może należeć do części wspólnej
30 wrz 17:45
Sympleks: wystarczyło wytłumaczyć że spójnik "i" oznacza część wspólną
gdyby zamiast "i" pojawiło się "lub" odpowiedzią byłby zbiór (−∞;6)
tak jak w poprzednim przykładzie tego samego zadania ze zbioru Andrzeja Kiełbasy
30 wrz 18:19
Aga1.: Tak też zrobiłam.
30 wrz 18:21
Sympleks: post był skierowany do Basi
30 wrz 18:35
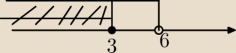
 ] do 6 (wyłączając również 6)
nie rozumiem dlaczego odpowiedzią w książce jest zbiór (−∞;3>, dlaczego przedział (3;6) nie
należy do tego zbioru
Bardzo ale to bardzo byłbym wdzięczny gdyby ktoś mi to wytłumaczył
] do 6 (wyłączając również 6)
nie rozumiem dlaczego odpowiedzią w książce jest zbiór (−∞;3>, dlaczego przedział (3;6) nie
należy do tego zbioru
Bardzo ale to bardzo byłbym wdzięczny gdyby ktoś mi to wytłumaczył

 Część wspólna, tam gdzie powstała kratka.Jeśli jest spójnik i, to wyznaczasz część wspólną, a
jeśli spójnik lub wówczas wyznaczasz sumę.
Liczba należy do części wspólnej, jeśli należy do obu zbiorów jednocześnie.
x≤3, czyli x∊(−∞,3>
x<6, czyli x∊(−∞,6)
I teraz np. 5 należy do pierwszego przedziału?Nie, więc nie może należeć do części wspólnej
Część wspólna, tam gdzie powstała kratka.Jeśli jest spójnik i, to wyznaczasz część wspólną, a
jeśli spójnik lub wówczas wyznaczasz sumę.
Liczba należy do części wspólnej, jeśli należy do obu zbiorów jednocześnie.
x≤3, czyli x∊(−∞,3>
x<6, czyli x∊(−∞,6)
I teraz np. 5 należy do pierwszego przedziału?Nie, więc nie może należeć do części wspólnej