Funkcje-kiełbasa Technik: Funkcja każdej liczbie naturalnej trzycyfrowej przyporządkowuje sumę jej cyfr. a)Podaj wszystkie argumenty dla których funkcja f przyjmuje wartość 2 b) Dla pewnego argumentu funkcja przyjmuje wartość 15. Uzasadnij, że a dzieli się przez 3 c) Podaj najmniejszą liczbę a taką, że f(a)=20 a) dla x={101,110,200} b) Liczba dzieli się przez 3 jeśli suma jej cyfr jest podzielna przez 3 więc a+b+c=15 tylko jak to ładnie zapisać ? c) 299

Basia: dobrze to co napisałeś w b) jest dobre, jasne i zupełnie wystarczające, ale jeżeli koniecznie chcesz to tak: x = 100*a+10*b+c f(x) = a+b+c f(x) = 15 ⇒ a+b+c = 15 ⇒ 3|(a+b+c) ⇒ 3|x

Technik: Dziękuję Basiu, masz jeszcze chwilkę ?

Basia: mam; jak coś masz to pisz tylko się nie zdziw jak jakiś idiotyzm napiszę; już mi się dzisiaj raz udało

Technik: Basia a ten mój zapis a+b+c=15 jest poprawny ? Funkcja g każdej liczbie x∊<−5,6> przyporządkowuje najmniejszą liczbę całkowitą n taką, że 3n jest większa od x a) podaj wartość funkcji g dla argumentów 0,−5, √2 b) Podaj miejsca zerowe funkcji g c) Podaj zbiór wartości a) g(0)=1 g(−5)=−1 g(√2)=1 b) MZ=(−3,0) (−2,0) (−1,0) c) ZW=C

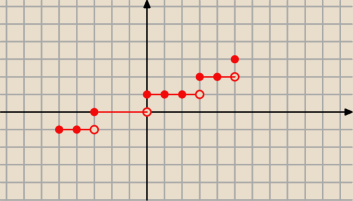
Basia: 1. jest poprawny 2. a) i b) dobrze c) nie najmniejsze x= −5 i f(−5) = −1 największe x=6 i f(6) = 3 ZW = {−1; 0; 1; 2; 3} to jest jej wykres

Technik: Basia ale tam jest przedział <−5,6> więc to chyba nie są wszystkie miejsca zerowe powinno być <−3,0) a odnośnie c ) ZW są przecież liczby całkowite ?

Basia: tak; zb.miejsc zerowych to <−3;0) myślałam, że chodzi tylko o całkowite; nie doczytałam ad.c oczywiście, że całkowite, ale przecież nie wszystkie; tylko pięć należy do ZW −1; 0; 1; 2; 3 ZW = {−1; 0; 1; 2; 3} czyli zbiór, do którego tych pięć liczb należy

Technik: No to lecimy dalej: Funkcja f każdej liczbie rzeczywistej x przyporządkowuje najmniejszą liczbę nieujemną a taką, że x+a jet liczbą całkowitą podzielną przez 4 a) Jaką wartość przyjmuję funkcja f dla argumentu −10,5, a jaką dla argumentu √2 b) ile jest miejsc zerowych funkcji f należących do przedziału <1,100> c) Podaj zbiór wartości d) Uzasadnij, że dla każdej liczby naturalnej n suma f(n)+f(n+1)+f(n+2)+f(n+3) ma stałą wartość a) f(−10,5)=−2,5 f(√2)=4−√2 b) a₁=4 a₂=8 r=4 a_n=100 n=25 miejsc zerowych c) ten nieszczęsny zbiór wartości C ? d) tego nie wiem

Basia: najmniejszą liczbę nieujemną (a) −2,5 jest ujemne −10,5+2,5 = −8 i jest podzielna przez 4 f(−10,5) = 2,5 f(√2) dobrze (b) dobrze (c) <0; +∞) (d) spośród liczb: n; n+1; n+2; n+3 dokładnie jedna jest podzielna przez 4, dokładnie jedna daje resztę 1; dokładnie jedna resztę 2 i dokładnie jedna resztę 3 no to mamy: f(n)+f(n+1)+f(n+2)+f(n+3) = 0+1+2+3 = 6 (dla formalności; to może być 1+2+3+0 lub 2+3+0+1 lub 3+0+1+2, ale to przecież już nie ma znaczenia)

Technik: Funkcja f każdej liczbie naturalnej n przyporządkowuje liczbę jej cyfr potrzebnych do jej zapisania w zapisie dziesiętnym a) Podaj zbiór wartości ZW=N b) Dla ilu argumentów funkcja przyjmuję wartość 3−dla 900 argumentów c) Podaj wszystkie argumenty n<3000 dla których zachodzi równość f(n+1)=f(n)+1

Technik: Basia tam się pomyliłem oczywiście powinno być 2,5 ale zbiór wartości <0,∞) ?

Basia: o Chryste Panie ZW = <0;4)

Technik: ZW ten zbiór wartości oczywiście do zadania 21:51 ma się rozumieć ?

Basia: tak; oczywiście

Technik: Ale czemu <0,4) otwarty przy 4 ?

Technik: Jak byś jeszcze miała czas to spójrz na zadanie 22:03 ?

Basia: otwarty; jeżeli x+4 jest podzielne przez 4 ⇒ samo x też czyli f(x) = 0 patrzę na to z 22:03

Basia: tutaj wszystko zależy od interpretacji czy do zapisania liczby 111 potrzebuję trzech cyfr czy jednej (trzech miejsc na pewno, ale czy trzech cyfr ?) czy do napisania liczby 10¹⁵⁰ potrzebuję 151 cyfr, czy dwóch ? jest to tam jakoś doprecyzowane ?

Technik: Zadanie podałem dokładnie ale chyba pierwsza wersja ?

Basia: zobacz w odpowiedziach jaka jest odpowiedź do (b) jeżeli 900 to pierwsza; jeżeli 9*9*8 = 81*8 = 648 to druga też się skłaniam do pierwszej, bo w wersji drugiej (c) byłoby bardzo trudne

Technik: 900

Basia: czyli wersja pierwsza (a) N₊ (nie ma liczb zerocyfrowych) (b) 900 (c) 9 i 10; 99 i 100; 999 i 1000;

Technik: Ale jak zrobić ten punkt c) ?

Basia: nijak nie robić; tylko pomyśleć wartość tej funkcji zmienia się gdy "przeskakujesz" z liczb jednocyfrowych na dwucyfrowe z dwucyfrowych na trzycyfrowe z trzycyfrowych na czterocyfrowe i tak dalej bierzesz dwie kolejne liczby: n i n+1 to albo mają tyle samo cyfr i wtedy f(n+1)=f(n) albo ta n+1 ma o jedną cyfrę więcej no to masz tylko te trzy pary w przedziale <0;3000> w ogóle jest ich nieskończenie wiele 9 i 10; 99 i 100; 999 i 1000; 9999 i 10000; 99999 i 100000 ;..................... ogólnie są to party: 10ⁿ−1 i 10ⁿ gdzie n∊N₊

bezendu: f(9+1)=2 f(9)+1=2 f(99+1)=3 f(99)+1=3 f(999+1)=4 f(999)+1=4

Technik: Basia dziękuję