Rozwiąż nierówność trygonometryczną marta: Rozwiąż nierówność trygonometryczną |sinx| ≥ |cosx|

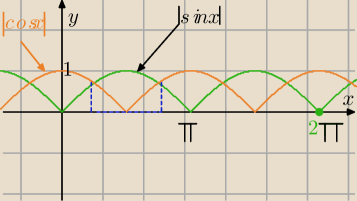
Mila: |sinx| ≥ |cosx|⇔

	π		3π
x∊<		+kπ,		+kπ>
	4		4

Saizou : lsinxl≥lcosxl /², bo L i P≥0 sin²x≥cos²x 0≥cos²x−sin²x cos2x≤0

π		3π
	+2kπ≤2x≤		+2kπ
2		2

π		3π
	+kπ≤x≤		+kπ
4		4

	π		3π
x∊<		+kπ;		+kπ>, k∊C
	4		4

PW: Można też podzielić

	sinx
|		| ≥ 1
	cosx

|tgx| ≥ 1 − wtedy rysunek jest łatwiejszy, bo tylko jedna funkcja. Trzeba jednak opisać sytuację, gdy cosx=0 i tego dzielenia wykonać nie można.

marta: dziękuję

Mila:

Basia: cosx = 0 i sinx = 1 dla każdego x=^π₂+2kπ 1 ≥ 0 |sinx| ≥ |cosx| nierówność jest spełniona, a tangens nie istnieje te rozwiązania z nierówności |tgx|≥ 1 nie wyjdą tak samo jak rozwiązania x = ^3π₂+2kπ cosx = 0 i sinx = −1 bezprawne dzielenie przez możliwe zero

Saizou : rozwiązań od koloru do wyboru

Basia: Twoje Saizou jest bardzo zgrabne Łatwo już rozwiązać tę nierówność cos2x≤0 Tak trzymaj