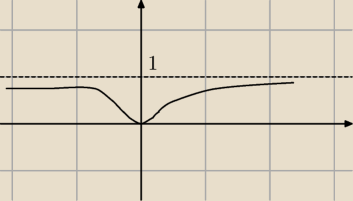
 Mam mniej więcej taką funkcję (normalnie jest parzysta, ale nie wyszło :<). Ciekawi mnie jej
wzór i jak można przedstawić jej logarytm naturalny.
Mam mniej więcej taką funkcję (normalnie jest parzysta, ale nie wyszło :<). Ciekawi mnie jej
wzór i jak można przedstawić jej logarytm naturalny.
| 1 | ||
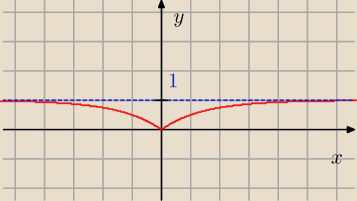
Przykładowo a = | wykres y = −(a)|x| + 1 wygląda tak | |
| 2 |
| 1 | ||
y = −( | )|x| + 1. | |
| 2 |
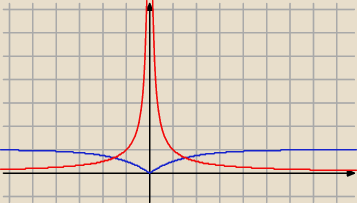 niebieskie to wykres: f(x) = −(12)|x| + 1
ln(f(x) to mniej więcej coś takiego jak to czerwone
prawie bo oszukałam trochę
niebieskie to wykres: f(x) = −(12)|x| + 1
ln(f(x) to mniej więcej coś takiego jak to czerwone
prawie bo oszukałam trochę
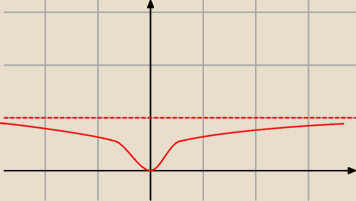 mnie się jednak wydaje, że to jest inna funkcja
różniczkowalna w zerze (a te "nasze" nie są, mają w zerze ostrze)
i ma dwa symetryczne punkty przegięcia
coś takiego; tylko wzoru nie mogę dopasować, ale wiem, że istnieje
mnie się jednak wydaje, że to jest inna funkcja
różniczkowalna w zerze (a te "nasze" nie są, mają w zerze ostrze)
i ma dwa symetryczne punkty przegięcia
coś takiego; tylko wzoru nie mogę dopasować, ale wiem, że istnieje
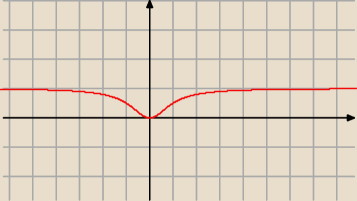
| x2 | ||
już mam; to jest f(x) = | ||
| x2+1 |
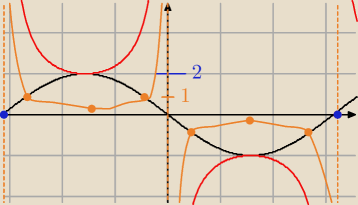 Mam jeszcze taką funkcję zbliżoną do sin x. Ograniczona jest domeną do niebieskich punktów
włącznie (tam x=0), maksymalna wartosc = 2, min. = −2. Czy wtedy funkcja odwrotna będzie też
podobna do 1/(−sin x), tak jak narysowałem pomarańczowym?
Mam jeszcze taką funkcję zbliżoną do sin x. Ograniczona jest domeną do niebieskich punktów
włącznie (tam x=0), maksymalna wartosc = 2, min. = −2. Czy wtedy funkcja odwrotna będzie też
podobna do 1/(−sin x), tak jak narysowałem pomarańczowym?
 Wykres funkcji odwrotnej do f(x) (o ile ta odwrotna istnieje) jest symetryczny
do wykresu y=f(x) względem prostej y = x.
Jest tak dlatego:
f: x→y to f−1:y → x
czyli jeżeli do wykresu f należy P(x,y) to do wykresu f−1 należy P(y,x)
a to właśnie jest symetria względem prostej y=x
Odgadywanie wzoru funkcji nie jest więc w ogóle potrzebne.
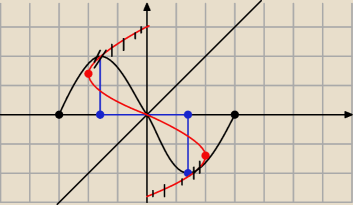
Co do Twojego rysunku to ta funkcja nie jest różnowartościowa.
Funkcja do niej odwrotna nie istnieje.
Można zbudować funkcję odwrotną tylko rozpatrując f(x) w tym niebieskim przedziale.
I to byłoby to czerwone, ale tylko od kropki do kropki.
Wykres funkcji odwrotnej do f(x) (o ile ta odwrotna istnieje) jest symetryczny
do wykresu y=f(x) względem prostej y = x.
Jest tak dlatego:
f: x→y to f−1:y → x
czyli jeżeli do wykresu f należy P(x,y) to do wykresu f−1 należy P(y,x)
a to właśnie jest symetria względem prostej y=x
Odgadywanie wzoru funkcji nie jest więc w ogóle potrzebne.
Co do Twojego rysunku to ta funkcja nie jest różnowartościowa.
Funkcja do niej odwrotna nie istnieje.
Można zbudować funkcję odwrotną tylko rozpatrując f(x) w tym niebieskim przedziale.
I to byłoby to czerwone, ale tylko od kropki do kropki.